题目内容
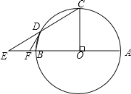
【题目】如图,直线BC与半径为6的⊙O相切于点B,点M是圆上的动点,过点M作MC⊥BC,垂足为C,MC与⊙O交于点D,AB为⊙O的直径,连接MA、MB,设MC的长为x,(6<x<12).
(1)当x=9时,求BM的长和△ABM的面积;
(2)是否存在点M,使MDDC=20?若存在,请求出x的值;若不存在,请说明理由.
【答案】(1)BM=6![]() ;S△ABM=18
;S△ABM=18![]() ;(2)不存在;理由见解析.
;(2)不存在;理由见解析.
【解析】
(1)利用切线的性质以及平行线的性质进而得出∠BMC=∠ABM以及∠BCM=∠AMB=90°,即可得出△BCM∽△AMB,根据相似三角形的性质即可求得BM的长,根据勾股定理求得BC,然后根据三角形面积公式求得△ABM的面积;
(2)首先得出四边形OBCE为矩形,进而得出MDDC=2(x-6)(12-x),进而求出最值即可判定.
(1)∵直线BC与半径为6的⊙O相切于点B,且AB为⊙O的直径,
∴AB⊥BC,
又∵MC⊥BC,
∴AB∥MC,
∴∠BMC=∠ABM,
∵AB是⊙O的直径,
∴∠AMB=90°,
∴∠BCM=∠AMB=90°,
∴△BCM∽△AMB,
∴![]() ,
,
∴BM2=ABMC=12×9=108,
∴BM=6![]() ,
,
∵BC2+MC2=BM2 ,
∴BC=![]() =3
=3![]()
∴S△ABM=![]() ABBC=
ABBC=![]() ×12×3
×12×3![]() =18
=18![]() ;
;
(2)过O作OE⊥MC,垂足为E,
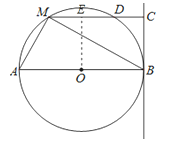
∵MD是⊙O的弦, OE⊥MD,
∴ME=ED,
又∵∠CEO=∠ECB=∠OBC=90°,
∴四边形OBCE为矩形,
∴CE=OB=6,
又∵MC=x,
∴ME=ED=MC﹣CE=x﹣6,MD=2(x﹣6),
∴CD=MC﹣MD=x﹣2(x﹣6)=12﹣x,
∴MDDC=2(x﹣6)(12﹣x)=﹣2x2+36x﹣144=﹣2(x﹣9)2+18
∵6<x<12,
∴当x=9时,MDDC的值最大,最大值是18,
∴不存在点M,使MDDC=20.