Question

【题目】如图，为的直径，于，在上，连接，，延长与的延长线交于，在上，且．

求证：是的切线；

若，，求的长．

Answer 1

【答案】（1）详见解析；（2）．

【解析】

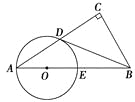
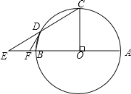
（1）连结OD，由CO⊥AB得∠E+∠C=90°，根据等腰三角形的性质由FE=FD，OD=OC得到∠E=∠FDE，∠C=∠ODC，于是有∠FDE+∠ODC=90°，则可根据切线的判定定理得到FD是⊙O的切线；

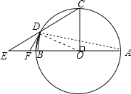
（2）连结AD，如图，利用圆周角定理，由AB为⊙O的直径得到∠ADB=90°，则∠A+∠ABD=90°，加上∠OBD=∠ODB，∠BDF+∠ODB=90°，则∠A=∠BDF，易得△FBD∽△FDA，根据相似的性质得，再在Rt△ABD中，根据正切的定义得到tan∠A=tan∠BDF==，于是可计算出DF=2，从而得到EF=2．

连结，如图，

∵，

∴，

∵，，

∴，，

∴，

∴，

∴，

∴是的切线；

连结，如图，

∵为的直径，

∴，

∴，

∵，

∴，

∴，

∵，

∴，

而，

∴，

∴，

在中，，

∴，

∴，

∴．