Question

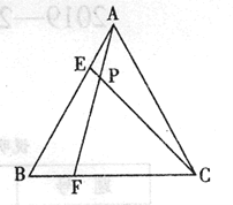
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=BC，点D是BC的中点，CE⊥AD，垂足为点E，BF∥AC交CE的延长线于点F．

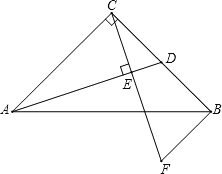
求证：（1）AC=2BF；

（2）AB垂直平分DF．

Answer 1

【答案】（1）证明见解析；（2）证明见解析．

【解析】

（1）易证∠CDA=∠F，即可证明△ACD≌△CBF，可得CD=BF，易证AC=2CD，即可解题；

（2）连接DF交AB于G点，易证BD=BF，∠ABC=45°，根据△ACD≌△CBF，可求得∠ABF=45°，即可证明∴△DBG≌△FBG，可得DG=FG，∠DGB=∠FGB，即可求得∠DGB=∠FGB=90°，即可解题．

解：（1）∵BF∥AC，∠ACB=90°，

∴∠CBF=∠ACB=90°

∴BC⊥BF，

又∵CE⊥AD，

∴∠DCE+∠F=90°，∠DCE+∠CDA=90°，

∴∠CDA=∠F，

在△ACD和△CBF中， ，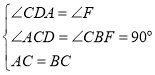

∴△ACD≌△CBF（AAS），

∴CD=BF，

∵点D是BC的中点，

∴BC=2CD=2BF，

又∵AC=BC

∴AC=2BF；

（2）连接DF交AB于G点，

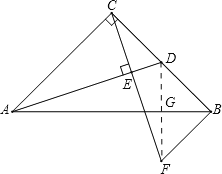
∵点D是BC的中点，

∴AC=2BD，

∵AC=2BF，

∴BD=BF，

∵AC=BC，∠ACB=90°，

∴∠ABC=45°，

∵△ACD≌△CBF，

∴∠CBF=∠ACD=90°，

∴∠ABF=45°，

在△DBG和△FBG中，，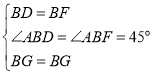

∴△DBG≌△FBG（SAS），

∴DG=FG，∠DGB=∠FGB，

∵∠DGB+∠FGB=180°，

∴∠DGB=∠FGB=90°，

∴AB垂直平分DF．