题目内容
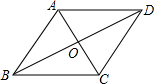 如图,?ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,BD=8.则?ABCD的周长为( )
如图,?ABCD的两条对角线AC、BD相交于点O,AB=5,AC=6,BD=8.则?ABCD的周长为( )分析:首先根据平行四边形的对角线互相平分,求得OA=3,OB=4.在三角形AOB中,根据勾股定理的逆定理可判定三角形AOB是直角三角形.再根据对角线互相垂直的平行四边形是菱形,得到平行四边形ABCD是菱形.根据菱形的四条边都相等,从而求得该四边形的周长.
解答:解:由平行四边形的性质得:OA=
AC=3,OB=
BD=4,
在△AOB中,∵OB2+OA2=AB2,
∴△AOB是直角三角形
∴AC⊥BD,
∴平行四边形ABCD是菱形,
故此四边形的周长为5×4=20.
故选C.
| 1 |
| 2 |
| 1 |
| 2 |
在△AOB中,∵OB2+OA2=AB2,
∴△AOB是直角三角形
∴AC⊥BD,
∴平行四边形ABCD是菱形,
故此四边形的周长为5×4=20.
故选C.
点评:此题综合运用了平行四边形的性质、勾股定理的逆定理以及菱形的判定和性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图梯形ABCD的两底长为AD=6,BC=10,中线为EF,且∠B=90°,若P为AB上的一点,且PE将梯形ABCD分成面积相同的两区域,则△EFP与梯形ABCD的面积比为( )
如图梯形ABCD的两底长为AD=6,BC=10,中线为EF,且∠B=90°,若P为AB上的一点,且PE将梯形ABCD分成面积相同的两区域,则△EFP与梯形ABCD的面积比为( )| A、1:6 | B、1:10 | C、1:12 | D、1:16 |
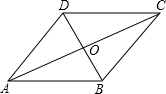 如图,?ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,BC=
如图,?ABCD的两条对角线AC和BD相交于点O,并且BD=4,AC=6,BC= 9、如图,?ABCD的两条对角线AC、BD相交于点O.
9、如图,?ABCD的两条对角线AC、BD相交于点O. 如图,?ABCD的两条对角线AC、BD相交于点O,问图中全等的三角形有哪几对?
如图,?ABCD的两条对角线AC、BD相交于点O,问图中全等的三角形有哪几对? 如图,?ABCD的两条对角线AC、BD相交于点O,那么,图中有几对三角形全等( )
如图,?ABCD的两条对角线AC、BD相交于点O,那么,图中有几对三角形全等( )