题目内容
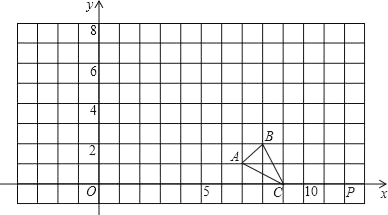
【题目】抛物线![]() 与x轴交于点A、B(点A在点B的左边), 点P在抛物线上.
与x轴交于点A、B(点A在点B的左边), 点P在抛物线上.
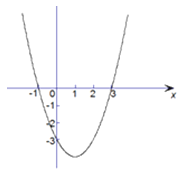
(1)点C是x轴上一个动点,四边形ACPQ是正方形,则满足条件 的点Q的坐标是______.
(2)连结AP,以AP为一条对角线作平行四边形AMPN,使点M在 以点(1,0),(0,1)为端点的线段上,则当点N的纵坐标取最小值时,N的坐标为______.
【答案】(-1,-3)或(-1,5) (0,-5)
【解析】
(1)AC是正方形的一边,如图所示:设点![]() 则点
则点![]()
![]()
![]() 根据正方形的边长相等,列出方程求解即可.
根据正方形的边长相等,列出方程求解即可.
(2)当点P在抛物线的顶点,点M在点![]() 时,点N的纵坐标最小,画出示意图,求解即可.
时,点N的纵坐标最小,画出示意图,求解即可.
(1) AC是正方形的一边,如图所示:
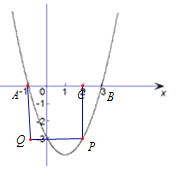
设点![]() 则点
则点![]()
![]()
![]()
![]()
则,![]()
解得:![]() 或
或![]() ,
,
当![]() 时,
时,![]() 点
点![]()
当![]() 时,
时,![]() 点
点![]()
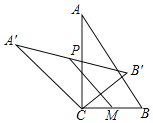
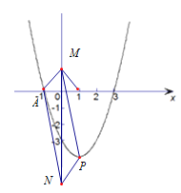
(2) 当点P在抛物线的顶点,点M在点![]() 时,点N的纵坐标最小,如图所示:
时,点N的纵坐标最小,如图所示:
![]() 则
则![]()
![]()
直线AM所在直线的方程为:![]()
设点N![]()
![]()
![]()
![]()
则: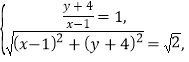
解得:![]()
![]() 舍去
舍去
即点N的坐标为![]()
故答案为:(1). (-1,-3)或(-1,5) (2). (0,-5)

练习册系列答案
相关题目
【题目】甲、乙两人参加射击比赛,两人成绩如图所示.
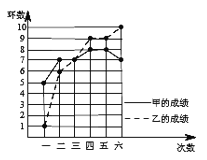
(1)填表:
平均数 | 方差 | 中位数 | 众数 | |
甲 | 7 | 1 | 7 | |
乙 | 9 |
(2)只看平均数和方差,成绩更好的是 .(填“甲”或“乙”)
(3)仅就折线图上两人射击命中环数的走势看,更有潜力的是 .(填“甲”或“乙”)