题目内容
【题目】如图，在Rt△ABC中，∠ACB=90°，点D，E分别是边AB，AC的中点，延长BC到点F，使CF= 
BC．若AB=10，则EF的长是 ． 
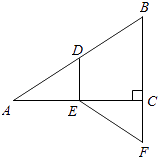
【答案】5
【解析】解：如图，连接DC． DE是△ABC的中位线，
∴DE∥BC，DE= 
，
∵CF= 
BC，
∴DE∥CF，DE=CF，
∴CDEF是平行四边形，
∴EF=DC．
∵DC是Rt△ABC斜边上的中线，
∴DC= 
=5，
∴EF=DC=5，
所以答案是：5．
【考点精析】关于本题考查的直角三角形斜边上的中线和三角形中位线定理，需要了解直角三角形斜边上的中线等于斜边的一半；连接三角形两边中点的线段叫做三角形的中位线；三角形中位线定理：三角形的中位线平行于三角形的第三边，且等于第三边的一半才能得出正确答案．
练习册系列答案
相关题目
【题目】某校组织学生到距离学校6千米的科技馆去参观，小华因事没能乘上学校的包车，于是准备在学校门口改乘出租车去科技馆，出租车收费标准有两种类型，如下表：
里程 | 甲类收费（元） | 乙类收费（元） |
3千米以下（包含3千米） | 7.00 | 6.00 |
3千米以上，每增加1千米 | 1.60 | 1.40 |
（1）设出租车行驶的里程为x千米（
且x取正整数），分别写出两种类型的总收费（用含x的代数式表示）；
（2）小华身上仅有11元，他乘出租车到科技馆车费够不够请说明理由．
【题目】八（2）班组织了一次经典朗读比赛，甲、乙两队各10人的比赛成绩如下表（10分制）：
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
（1）甲队成绩的中位数是分，乙队成绩的众数是分；
（2）计算乙队的平均成绩和方差；
（3）已知甲队成绩的方差是1.4分2 ， 则成绩较为整齐的是队．