题目内容
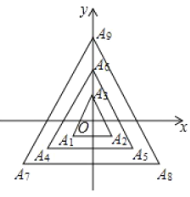
【题目】如图， A1A2 A3 ， A4 A5 A6 ， A7 A8 A9 ，
， A3n2 A3n1A3n（n 为正整数）均为等边三角形，它们的边长依次是 2，4，6，，2n，顶点 A3，A6，A9，A3n 均在 y 轴上，点 O 是所有等边三角形的中心，点 A2020的坐标为_________．
【答案】（-674，-
）
【解析】
先关键等边三角形的性质和已知条件得出A1的坐标，根据每一个三角形有三个顶点确定出A2020所在的三角形，再求出相应的三角形的边长以及A2020的横纵坐标的长度，即可得解．
∵A1A2 A3 ， A4 A5 A6 ， A7 A8 A9 ，
， A3n2 A3n1A3n（n 为正整数）均为等边三角形，它们的边长依次是 2，4，6，，2n，
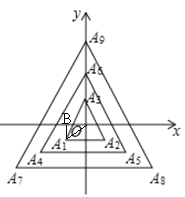
过A1作A1B⊥x轴于B点，
∵点O是所有等边三角形的中心，
∴∠A1OB=30°
∵A1A2=2，
∴OB=
A1A2=1
A1B=OBtan30°=1×
=
∴A1(-1,- )
同理A4A5=4
则第二个三角形第1个顶点A4（-2，- 
）
同理第三个三角形第1个顶点A7（-3，- 
）
2020÷3＝673…1
∴A2020是第674个等边三角形的第1个顶点，位于第三象限
∴点A2020的坐标为（-1×674，-674×）
即（-674，-）
故答案为：（-674，-）．
练习册系列答案
名校课堂系列答案
相关题目
