Question

【题目】抛物线y＝﹣x2+x﹣1与x轴交于点A，B(点A在点B的左侧)，与y轴交于点C，其顶点为D．将抛物线位于直线l：y＝t(t＜)上方的部分沿直线l向下翻折，抛物线剩余部分与翻折后所得图形组成一个“M”形的新图象．

(1)点A，B，D的坐标分别为　 　，　 　，　 　；

(2)如图①，抛物线翻折后，点D落在点E处．当点E在△ABC内(含边界)时，求t的取值范围；

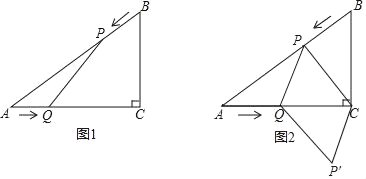
(3)如图②，当t＝0时，若Q是“M”形新图象上一动点，是否存在以CQ为直径的圆与x轴相切于点P？若存在，求出点P的坐标；若不存在，请说明理由．

[Failed to download image : http://192.168.0.10:8086/QBM/2019/5/28/2213337932849152/2214008649842688/STEM/890e59b444e5404588b8511540e03e41.png]

Answer 1

【答案】（1）A（，0）；B（3，0）；D（，）；（2）≤t≤；（3）存在以CQ为直径的圆与x轴相切于点P，点P的坐标为（，0）、（，0）、（1，0）或（，0）．

【解析】

（1）利用二次函数图像上的点的坐标特征可求得点A、B的坐标，再利用配方法即可找到抛物线的顶点坐标；

（2）由点D的坐标结合对称找到点E的坐标，根据点B、C的坐标利用待定系数法确定直线BC函数关系式，再利用一次函数图像上的坐标特征即可得出关于t的一元一次不等式组，解之即可得出t的取值范围；

（3）假设存在，设点P的坐标为（，0），则点Q的横坐标为m，分或及三种情况，利用勾股定理找出关于m的一元二次方程，解出即可得出m的值，进而可找出点P的坐标.

解：（1）当y=0时，﹣x2+x﹣1=0，

解得x1=,x2=3,

∴点A的坐标为（，0），点B的坐标为（3,0），

∵y=﹣x2+x﹣1=﹣（x-）2+,

∴点D的坐标为（，）；

（2）∵点E、点D关于直线y=t对称，

∴点E的坐标为（，2t﹣）．

当x=0时，y=﹣x2+x﹣1=﹣1，

∴点C的坐标为（0，﹣1）．

设线段BC所在直线的解析式为y=kx+b，

将B（3，0）、C（0，﹣1）代入y=kx+b，

，解得：，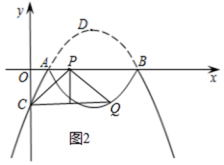

∴线段BC所在直线的解析式为y=x﹣1．

∵点E在△ABC内（含边界），

∴，

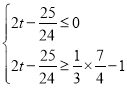解得：≤t≤．

（3）当x＜或x＞3时，y=﹣x2+x﹣1；

当≤x≤3时，y=﹣x2+x﹣1．

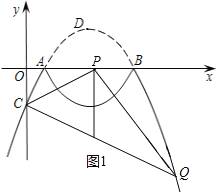
假设存在，设点P的坐标为（m，0），则点Q的横坐标为m．

①当m＜或m＞3时，点Q的坐标为（m，﹣x2+x﹣1）（如图1），

∵以CQ为直径的圆与x轴相切于点P，

∴CP⊥PQ，

∴CQ2=CP2+PQ2，

即m2+（﹣m2+m）2=m2+1+m2+（﹣m2+m﹣1）2，

整理，得：m1=，m2=，

∴点P的坐标为（，0）或（，0）；

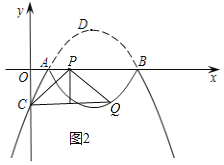
②当≤m≤3时，点Q的坐标为（m,x2-x +1）（如图2），

∵以CQ为直径的圆与x轴相切于点P，

∴CP⊥PQ，

∴CQ2=CP2+PQ2，即m2+（m2﹣m+2）2=m2+1+m2+（m2﹣m+1）2，

整理，得：11m2﹣28m+12=0，

解得：m3=，m4=2，

∴点P的坐标为（，0）或（1，0）．

综上所述：存在以CQ为直径的圆与x轴相切于点P，点P的坐标为（，0）、（，0）、（1，0）或（，0）．