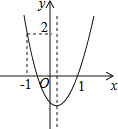Question

【题目】如图，已知抛物线y=x2﹣x﹣3与x轴的交点为A、D（A在D的右侧），与y轴的交点为C．

（1）直接写出A、D、C三点的坐标；

（2）若点M在抛物线上，使得△MAD的面积与△CAD的面积相等，求点M的坐标；

（3）若点P是抛物线对称轴上一点，在抛物线上是否存在一点Q，使以A,D,P,Q为顶点的四边形是平行四边行？若存在，求出Q点的坐标，若不存在，请说明理由．

Answer 1

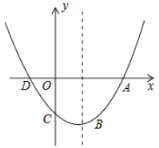
【答案】（1）A点坐标为（4，0），D点坐标为（2，0），C点坐标为（0，3）；（2）M点坐标为（2，3）或（1＋，3）或（1，3）；(3) Q（1，-）或Q (7, )或Q (-5, )

【解析】

（1）令y＝0，解方程x2﹣x﹣3＝0可得到A点和D点坐标；令x＝0，求出y＝3，可确定C点坐标；

（2）根据抛物线的对称性，可知在在x轴下方对称轴右侧也存在这样的一个点；再根据三角形的等面积法，在x轴上方，存在两个点，这两个点分别到x轴的距离等于点C到x轴的距离；

（2）分AD是平行四边形的边和对角线分别作图，根据图形的特点即可求解．

（1）∵y＝x2﹣x﹣3，

∴当y＝0时，

x2﹣x﹣3＝0，

解得x1＝2，x2＝4．

当x＝0，y＝3．

∴A点坐标为（4，0），D点坐标为（2，0），C点坐标为（0，3）；

（2）∵y＝x2﹣x﹣3

∴对称轴为直线x＝．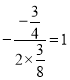

∵AD在x轴上，点M在抛物线上，

∴当△MAD的面积与△CAD的面积相等时，分两种情况：

①点M在x轴下方时，根据抛物线的对称性，可知点M与点C关于直线x＝1对称，

∵C点坐标为（0，3），

∴M点坐标为（2，3）；

②点M在x轴上方时，根据三角形的等面积法，可知M点到x轴的距离等于点C到x轴的距离3．

当y＝3时，x2﹣x﹣3＝3，

解得x1＝1＋，x2＝1，

∴M点坐标为（1＋，3）或（1，3）．

综上所述，所求M点坐标为（2，3）或（1＋，3）或（1，3）；

(3)如图，当AD是平行四边形的一边时，

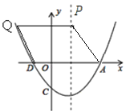
设Q(x, x2﹣x﹣3)，则P（1，x2﹣x﹣3）

由AD==4-(-2)=6，得

解得x=7或x=-5

故Q (7, )，P（1，）或Q (-5, )，P（1，）

如图，当AD是平行四边形的对角线时，设PQ,AD交于H点，

则P,Q在对称轴x=1上，

∵x=1时，y=x2﹣x﹣3=-

∴HQ=PH=

故Q（1，-），P（1，）

综上，存在Q（1，-）或Q (7, )或Q (-5, )，使得以点A、D、P、Q为顶点的四边形是平行四边形．