题目内容
【题目】如图,在边长为4的正方形ABCD中,对角线AC,BD相交于点O,点E是AD边上一点,连接CE,把△CDE沿CE翻折,得到△CPE,EP交AC于点F,CP交BD于点G,连接PO,若PO∥BC,则四边形OFPG的面积是 . 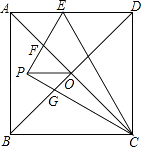
【答案】8﹣4 ![]()
【解析】解:如图所示,过P作PM⊥AO于M,作PN⊥BO于N,延长PO交CD于H,
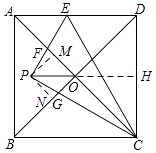
∵PO∥BC,BC⊥CD,
∴PH⊥CD,
又∵△CDO是等腰直角三角形,
∴OH= ![]() CD=2=CH,OH平分∠COD,
CD=2=CH,OH平分∠COD,
由折叠可得,CP=CD=4,
∴Rt△PCH中,PH= ![]() =2
=2 ![]() ,
,
∴PO=PH﹣OH=2 ![]() ﹣2,
﹣2,
∵PO平分∠AOB,PM⊥AO,PN⊥BO,
∴PM=PN,
矩形PMON是正方形,
∴正方形PMON的面积= ![]() OP2=
OP2= ![]() (2
(2 ![]() ﹣2)2=8﹣4
﹣2)2=8﹣4 ![]() ,
,
∵∠FPG=∠MON=90°,
∴∠FPM=∠GPN,
在△PMF和△PNG中,
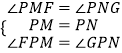 ,
,
∴△PMF≌△PNG(ASA),
∴S△PMF=S△PNG,
∴S四边形OFPG=S正方形PMON,
∴四边形OFPG的面积是8﹣4 ![]() ,
,
故答案为:8﹣4 ![]() .
.
通过做辅助线过P作PM⊥AO于M,作PN⊥BO于N,延长PO交CD于H,又因△CDO是等腰直角三角形,可得OH=2=CH,OH平分∠COD,由折叠的性质可得,CP=CD=4,有勾股定理可得PH =2 ![]() ,PO=PH﹣OH=2
,PO=PH﹣OH=2 ![]() ﹣2,得到正方形PMON的面积,得到△PMF≌△PNG(ASA),得到S△PMF=S△PNG,S四边形OFPG=S正方形PMON,求出四边形OFPG的面积是8﹣4
﹣2,得到正方形PMON的面积,得到△PMF≌△PNG(ASA),得到S△PMF=S△PNG,S四边形OFPG=S正方形PMON,求出四边形OFPG的面积是8﹣4 ![]() .
.

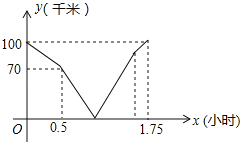
【题目】阅读对学生的成长有着深远的影响,某中学为了解学生每周课余阅读的时间,在本校随机抽取了若干名学生进行调查,并依据调查结果绘制了以下不完整的统计图表.
组别 | 时间(小时) | 频数(人数) | 频率 |
A | 0≤t≤0.5 | 6 | 0.15 |
B | 0.5≤t≤1 | a | 0.3 |
C | 1≤t≤1.5 | 10 | 0.25 |
D | 1.5≤t≤2 | 8 | b |
E | 2≤t≤2.5 | 4 | 0.1 |
合计 | 1 |
请根据图表中的信息,解答下列问题:
(1)表中的a= ,b= ,中位数落在 组,将频数分布直方图补全;
(2)估计该校2000名学生中,每周课余阅读时间不足0.5小时的学生大约有多少名?
(3)E组的4人中,有1名男生和3名女生,该校计划在E组学生中随机选出两人向全校同学作读书心得报告,请用画树状图或列表法求抽取的两名学生刚好是1名男生和1名女生的概率.