题目内容
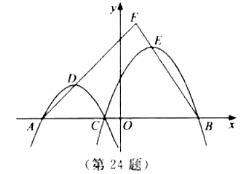
【题目】如图,在平面直角坐标系![]() 中,已知
中,已知![]() ,
,![]() 两点的坐标分别为
两点的坐标分别为![]() ,
,![]() ,
,![]() 是线段
是线段![]() 上一点(与
上一点(与![]() ,
,![]() 点不重合),抛物线
点不重合),抛物线![]()
![]() (
(![]() )经过点
)经过点![]() ,
,![]() ,顶点为
,顶点为![]() ,抛物线
,抛物线![]()
![]() (
(![]() )经过点
)经过点![]() ,
,![]() ,顶点为
,顶点为![]() ,
,![]() ,
,![]() 的延长线相交于点
的延长线相交于点![]() .
.
(1)若![]() ,
,![]() ,求抛物线
,求抛物线![]() ,
,![]() 的解析式;
的解析式;
(2)若![]() ,
,![]() ,求
,求![]() 的值;
的值;
(3)是否存在这样的实数![]() (
(![]() ),无论
),无论![]() 取何值,直线
取何值,直线![]() 与
与![]() 都不可能互相垂直?若存在,请直接写出
都不可能互相垂直?若存在,请直接写出![]() 的两个不同的值;若不存在,请说明理由.
的两个不同的值;若不存在,请说明理由.
【答案】(1)抛物线L1的解析式为y=![]() ,抛物线L2的解析式为y=
,抛物线L2的解析式为y=![]() (2)m=±2
(2)m=±2![]() (3)存在
(3)存在
【解析】
试题分析:(1)把a、m代入得到已知点,把点代入函数的解析式,然后构成方程组,根据待定系数法可求出函数的解析式;
(2)如图,过点D作DG⊥x轴于点G,过点E作EH⊥x轴于点H,把a=-1代入函数解析式,然后结合(m,0)和(-4,0)代入可求解出函数解析式L1,然后分别求出D点坐标,得到DG、AG的长,同理得到L2,求得EH,BH的长,再根据三角形相似的判定与性质构造方程求解即可;
(3)根据前面的解答,直接写出即可.
试题解析:(1)由题意得
解得
所以抛物线L1的解析式为y=![]()
同理,
解得
∴所以抛物线L2的解析式为y=![]()
(2)如图,过点D作DG⊥x轴于点G,过点E作EH⊥x轴于点H
由题意得
解得
∴抛物线L1的解析式为y=-x2+(m-4)x+4m
∴点D的坐标为(![]() ,
,![]() )
)
∴DG=![]() ,AG=
,AG=![]()
同理可得,抛物线L2的解析式为y=-x2+(m+4)x-4m
EH=![]() ,BH=
,BH=![]()

∵AF⊥BF,DG⊥x轴,EH⊥x轴
∴∠AFB=∠AGD=∠EHB=90°
∴∠ADG=∠ABF=90°-∠BAF
∴△ADG∽△EBH
∴![]()
∴
解得m=±2![]()
(3)存在,例如:a=-![]() ,a=-
,a=-![]() .(答案不唯一)
.(答案不唯一)

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目