Question

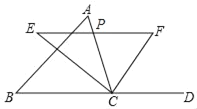
【题目】如图，△ABC中，点P是AC边上一个动点，过P作直线EF∥BC，交∠ACB的平分线于点E，交∠ACB的外角∠ACD平分线于点F．

（1）请说明：PE＝PF；

（2）当点P在AC边上运动到何处时，四边形AECF是矩形？为什么？

Answer 1

【答案】（1）详见解析；（2）当点P在AC中点时，四边形AECF是矩形，理由详见解析.

【解析】

(1)首先证明∠E=∠2根据等角对等边可得EP=PC，同理可得PF=PC，进而得到EP=PF；

(2)当点P在AC中点时，四边形AECF是矩形，首先根据对角线互相平分的四边形是平行四边形可得四边形AECF是平行四边形，再证明∠ECF=90°即可.

(1)∵CE平分∠BCA，

∴∠1＝∠2，

∵EF∥BC，

∴∠E＝∠1，

∴∠E＝∠2，

∴EP＝PC，

同理PF＝PC，

∴EP＝PF；

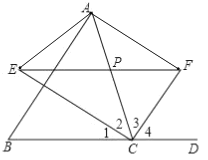
(2)结论：当点P在AC中点时，四边形AECF是矩形，

理由：∵PA＝PC，PE＝PF，

∴四边形AECF是平行四边形，

∵∠1=∠2，∠3=∠4，∠1+∠2+∠3+∠4=180°，

∴∠2+∠3=90°，

即∠ECF＝90°，

∴平行四边形AECF是矩形.