题目内容
【题目】实验室里,水平桌面上有甲、乙、丙三个高都为10cm圆柱形容器(甲、丙的底面积相同),用两个相同的管子在容器的6cm高度处连通(即管子底离容器底6cm,管子的体积忽略不计).现三个容器中,只有甲中有水,水位高2cm,如图①所示.若每分钟同时向乙、丙容器中注入相同量的水,到三个容器都注满水停止,乙、丙容器中的水位h(cm)与注水时间t(min)的图象如图②所示.若乙比甲的水位高2cm时,注水时间m分钟,则m的值为( )

A.3或5B.4或6C.3或![]() D.5或9
D.5或9
【答案】C
【解析】
确定![]() 、
、![]() 的值,再分乙容器的水位达到
的值,再分乙容器的水位达到![]() 时、甲容器的水位达到
时、甲容器的水位达到![]() 时两种情况,分别求解.
时两种情况,分别求解.
解:2分钟时,丙的水量达到6cm,而此时乙的水量为2cm,故乙、丙两容器的底面积之比为3:1,
∵乙、丙两容器的底面积之比为3:1,丙容器注入2分钟到达6cm,
∴乙容器的水位达到6cm所需时间为:a=2+2=4(min),
b=(10﹣2+10×3+10)÷6=8(min).
①当2≤x≤4时,设乙容器水位高度h与时间t的函数关系式为h=kt+b(k≠0),
∵图象经过(2,2)、(4,6)两点,则![]() ,解得:
,解得:![]() ,
,
∴h=2t﹣2(2≤x≤4).
当h=4时,则2t﹣2=4,解得t=3;
②设t分钟后,甲容器水位为4cm,根据题意得:2+6(t﹣4)=4,
解得:t=![]() .
.
故选:C.

 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
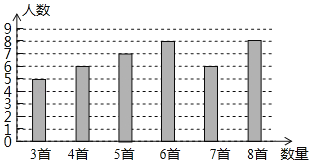
名校联盟快乐课堂系列答案【题目】某校组织全校1200名学生进行经典诗词诵读活动,并在活动之后举办经典诗词大赛,为了解本次系列活动的持续效果,学校团委在活动启动之初,随机抽取40名学生调查“一周诗词诵背数量”,根据调查结果绘制成的统计图如图所示.
大赛结束后一个月,再次抽查这部分学生“一周诗词诵背数量”,绘制成统计表如下:
一周诗词诵背数量 | 3首 | 4首 | 5首 | 6首 | 7首 | 8首 |
人数 | 1 | 3 | 5 | 6 | 10 | 15 |
请根据调查的信息
(1)估计大赛后一个月该校学生一周诗词诵背6首(含6首)以上的人数.
(2)选择适当的统计量,至少从两个不同的角度分析两次调查的相关数据,评价该校经典诗词诵背系列活动的效果.