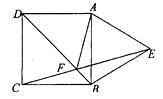
题目内容
【题目】如图,在ABCD中,∠BCD=120°,分别延长DC、BC到点E,F,使得△BCE和△CDF都是正三角形.
(1)求证:AE=AF;
(2)求∠EAF的度数.
【答案】(1)证明见试题解析;(2)60°.
【解析】
试题分析:(1)根据平行四边形的性质得到∠BAD=∠BCD=120°,∠ABC=∠ADC,AB=CD,BC=AD,根据等边三角形的性质得到BE=BC,DF=CD,∠EBC=∠CDF=60°,即可证出∠ABE=∠FDA,AB=DF,BE=AD,由SAS证明△ABE≌△FDA,得出对应边相等即可;
(2)根据全等三角形的性质得到∠AEB=∠FAD,求出∠AEB+∠BAE=60°,得出∠FAD+∠BAE=60°,即可得出∠EAF的度数.
试题解析:(1)∵四边形ABCD是平行四边形,∴∠BAD=∠BCD=120°,∠ABC=∠ADC,AB=CD,BC=AD,∵△BCE和△CDF都是正三角形,∴BE=BC,DF=CD,∠EBC=∠CDF=60°,∴∠ABE=∠FDA,AB=DF,BE=AD,在△ABE和△FDA中,∵AB=DF,∠ABE=JIAO FDA,BE=AD,∴△ABE≌△FDA(SAS),∴AE=AF;
(2)∵△ABE≌△FDA,∴∠AEB=∠FAD,∵∠ABE=60°+60°=120°,∴∠AEB+∠BAE=60°,∴∠FAD+∠BAE=60°,∴∠EAF=120°﹣60°=60°.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目