题目内容
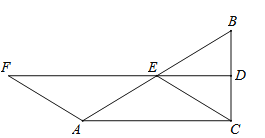
【题目】在矩形ABCD中AB=16，AD=12，点M是AD的中点，点N是CD的中点，点P从A点出发沿A→B→C→D的路线匀速运动，速度为2单位长度/秒，点Q从N点出发沿N→C→B→A的路线匀速运动，速度为1单位长度/秒，P、Q两点同时运动，时间为t秒，若其中一点到达终点，另一点也随即停止运动．
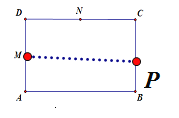
（1）如图1，若矩形ABCD与∠PMA重叠部分的面积为y．
①求当t=4，10，16时，y的值．
②求y关于t的函数解析式．
（2）当以M、D、P、Q四个点为顶点的四边形是平行四边形时，求出此时t的值．
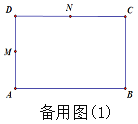
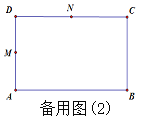
【答案】（1）①24，80，156. ②当
时，y=6t； 当
时，y=16t-80当
时，y=6t+60 （2）t=10， t=14
【解析】
试题（1））①首先确定t=4，10，16时P点所在的位置，然后根据重叠部分的形状，运用相应的面积公式即可求出对应的y值；
②由于点P在每一条边上运动的时间为6秒，所以分三种情况进行讨论：（Ⅰ）当0≤t≤8，即点P在边AB上时；（Ⅱ）当8＜t≤14，即点P在边BC上时；（Ⅲ）当14＜t≤22，即点P在边CD上时．针对每一种情况，都可以根据重叠部分的形状，运用相应的面积公式求出对应的y关于t的函数解析式；
(2)当P、Q在线段BC上时，分两种情况讨论当PB＜QB时和当PB＞QB时.
试题解析：
（1）①∵AD=12, 点M是AD的中点，
∴AM=6;
当t=4时，AP=8<16,故点P在AB上
∴y＝
；
当t=10时,点P路程为20,16<20<28,故点P在线段BC上
∴y＝
.
当t=16时，点P路程为32, 28<32<44,故点P在线段CD上
∴y＝
.
②当0<t
8时，点P在线段AB上，如图所示：
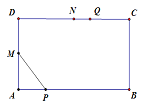
AP=2t,AM=
,
所以y=
;
当8<t14时，点P在线段BC上，如图所示：
BP＝2t-16,y=
.
当14<t22时，点P在线段CD上，如图所示：
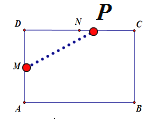
DP=44-2t,y=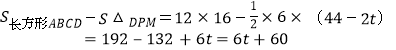
;
(2)P、Q两点都在线段BC上，当PB＜QB时，36-3t=6，t=10；
当PB＞QB时，3t-36=6，t=14 .
【题目】为参加学校的“我爱古诗词”知识竞赛，小王所在班级组织了一次古诗词知识测试，并将全班同学的分数（得分取正整数，满分为100分）进行统计．以下是根据这次测试成绩制作的不完整的频率分布表和频率分布直方图．
组别 | 分组 | 频数 | 频率 |
1 | 50≤x＜60 | 9 | 0.18 |
2 | 60≤x＜70 | a | |
3 | 70≤x＜80 | 20 | 0.40 |
4 | 80≤x＜90 | 0.08 | |
5 | 90≤x≤100 | 2 | b |
合计 |
请根据以上频率分布表和频率分布直方图，回答下列问题：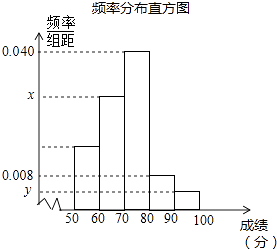
（1）求出a、b、x、y的值；
（2）老师说：“小王的测试成绩是全班同学成绩的中位数”，那么小王的测试成绩在什么范围内？
（3）若要从小明、小敏等五位成绩优秀的同学中随机选取两位参加竞赛，请用“列表法”或“树状图”求出小明、小敏同时被选中的概率．（注：五位同学请用A、B、C、D、E表示，其中小明为A，小敏为B）
