题目内容
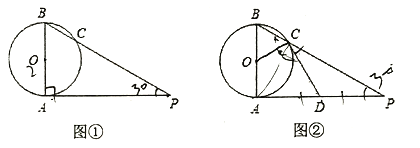
【题目】如图,已知一次函数y=mx+n的图像与x轴交于点B,与反比例函数![]() (k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(k﹥0)的图像交于点C,过点C作CH⊥x轴,点D是反比例函数图像上的一点,直线CD与x轴交于点A,若∠HCB=∠HCA,且BC=10,BA=16.
(1)若OA=11,求k的值;
(2)沿着x轴向右平移直线BC,若直线经过H点时恰好又经过点D,求一次函数函数y=mx+n的表达式.

【答案】(1)k=18;(2)![]() .
.
【解析】
(1)由∠HCB=∠HCA及CH⊥x轴得到△CHB≌△CHA,推出BH=HA=8,由BC=6根据勾股定理求出CH,由OA=11进而得出C点坐标,求得k值;
(2)过D点作DN⊥x轴于N点,由H是AB中点且HD∥BC得到D是AC的中点,设C点坐标,进而表示出D点坐标,根据k相等即可建立方程求解.
解:(1)∵CH⊥x轴
∴∠CHB=∠CHA=90°
在△CHB和△CHA中
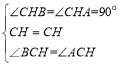 ,∴△CHB≌△CHA(ASA)
,∴△CHB≌△CHA(ASA)
∴BH=AH=![]() AB=8
AB=8
在△BCH中,由勾股定理可知:![]()
且OH=OA-AH=11-8=3
故C点的坐标为:(3,6)
∴反比例的k=3×6=18.
故答案为:18.
(2) 过D点作DN⊥x轴于N点,如下图所示:
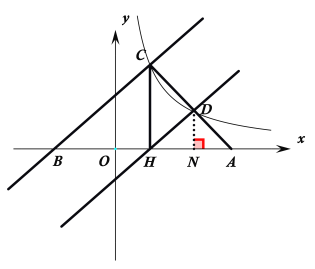
设C点坐标为(a,6),∴OH=a,CH=6
由HD∥BC,且H是AB的中点可知
HD是△ABC的中位线,且D是AC的中点
又DN⊥CH,∴DN∥CH
∴DN是△ACH的中位线
∴DN=![]() CH=4,HN=NA=
CH=4,HN=NA=![]() AH=4
AH=4
∴ON=OH+HN=a+4
∴D点的坐标为(a+4,3)
又∵C、D均在反比例函数上,
∴6×a=(a+4)×3
解之得:a=4,故C点坐标为(4,6)
BO=BH-OH=8-4=4,故B点坐标为(-4,0)
将C(4,6)和B(-4,0)代入y=mx+n中:
![]() ,解之得:
,解之得:![]()
故一次函数的解析式为:![]() .
.
故答案为:![]() .
.