题目内容
【题目】如图,抛物线 ![]() (m<0)的顶点为A,交y轴于点C.
(m<0)的顶点为A,交y轴于点C.
(1)求出点A的坐标(用含m的式子表示);
(2)平移直线y=x经过点A交抛物线C于另一点B,直线AB下方抛物线C上一点P,求点P到直线AB的最大距离
(3)设直线AC交x轴于点D,直线AC关于x轴对称的直线交抛物线C于E、F两点.若∠ECF=90°,求m的值.
【答案】
(1)
解:∵ ![]() ,
,
∴顶点A坐标 ![]()
(2)
解:∵直线AB的解析式为 ![]() ,
,
设P ![]() ,
,
过点P作PQ∥y轴交AB于Q,如图1中,

∴Q ![]()
∴PQ= ![]()
= ![]() ,
,
当 ![]() 时,PQ有最大值为
时,PQ有最大值为 ![]() ,
,
∵PQ与直线AB的夹角为45°
∴P到直线AB的距离d的最大值为 ![]() .
.
(3)
解:A(﹣m,﹣ ![]() m2+m)、C(0,m)
m2+m)、C(0,m)
A′(﹣m, ![]() m2﹣m,)、C′(0,﹣m)
m2﹣m,)、C′(0,﹣m)
∴直线EF的解析式为y=﹣ ![]() mx﹣m,
mx﹣m,
设E(x1,y1)、F(x2,y2)
过点C作MN∥x轴,过点E作EM⊥MN于M,过点F作FN⊥MN于N,
∵∠ECF=90°,
∴∠ECM+∠FCN=90°,∠FCN+∠CFN=90°,
∴∠ECM=∠CFN,∵∠EMC=∠FNC=90°,
∴Rt△EMC∽Rt△CNF,∴ ![]() ,
,
即 ![]() ,
,
化简得:y1y2﹣m(y1+y2)+m2=﹣x1x2
由 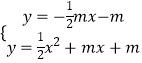 ,消去y,整理得:x2+3mx+4m=0
,消去y,整理得:x2+3mx+4m=0
∴x1+x2=﹣3m,x1x2=4m
y1y2=(﹣ ![]() mx1﹣m)(﹣
mx1﹣m)(﹣ ![]() mx2﹣m)=﹣
mx2﹣m)=﹣ ![]() m3+m2
m3+m2
y1+y2= ![]() m2﹣2m,
m2﹣2m,
∴﹣ ![]() m3+m2﹣m(
m3+m2﹣m( ![]() m2﹣2m)+m2=﹣4m,
m2﹣2m)+m2=﹣4m,
∴m(m-2m-2)=0
解得m=1- ![]() 或1+
或1+ ![]() 或0,
或0,
∵m<0,∴m=1- ![]() .
.
【解析】把抛物线的解析式写成顶点式的形式,表示出顶点;表示出PQ的距离,根据二次的函数的性质求最值。
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 阅读快车系列答案
阅读快车系列答案













