题目内容
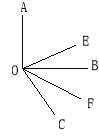
【题目】如图,已知∠AOB, OE平分∠AOC, OF平分∠BOC.

(1)若∠AOB是直角,∠BOC=60°,求∠EOF的度数;
(2)猜想∠EOF与∠AOB的数量关系;
(3)若∠AOB+∠EOF=156°,则∠EOF是多少度?
【答案】(1)45°;(2)∠EOF=![]() ∠AOB;(3)52°.
∠AOB;(3)52°.
【解析】
试题分析:(1)先求出∠AOC的度数,再根据角平分线的定义求出∠EOC与∠COF的度数,然后相减即可得解;
(2)设∠COF=x,∠EOB=y,先用x,y表示出∠EOF,再用x,y表示出∠AOB,然后得出两者的关系;
(3)根据(2)的规律,∠EOF的度数等于∠AOB的一半,进行求解即可.
试题解析:(1)∵∠AOB是直角,∠BOC=60°,∴∠AOC=∠AOB+∠BOC=90°+60°=150°,∵OE平分∠AOC,OF平分∠BOC,∴∠EOC=![]() ∠AOC=
∠AOC=![]() ×150°=75°,∠COF=
×150°=75°,∠COF=![]() ∠BOC=
∠BOC=![]() ×60°=30°,∴∠EOF=∠EOC﹣∠COF=75°﹣30°=45°;
×60°=30°,∴∠EOF=∠EOC﹣∠COF=75°﹣30°=45°;
(2)设∠COF=x,∠EOB=y,∵OE平分∠AOC,OF平分∠BOC,∴∠BOF= x,∠AOE=∠EOC=2x+y,∴∠EOF=x+y,∠AOB=2x+2y,∴∠EOF=![]() ∠AOB;
∠AOB;
(3)∵∠EOF=![]() ∠AOB,∴∠AOB=2∠EOF,∵∠AOB+∠EOF=156°,∴3∠EOF=156°,∴∠EOF=52°.
∠AOB,∴∠AOB=2∠EOF,∵∠AOB+∠EOF=156°,∴3∠EOF=156°,∴∠EOF=52°.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目