题目内容
【题目】如图，已知正方形ABCD的边长为2，△ABE时等边三角形，点E在正方形ABCD内，在对角线AC上有一点P，使PD+PE的和最小，则这个最小值为 ．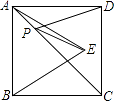 
【答案】2
【解析】解：设AC交BE于P′，连接DP′、PB．
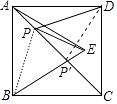
∵四边形ABCD是正方形，
∴B、D关于AC对称，
∴PD=PB，P′D=P′B，
∴PD+PE=PB+PE，
∴当P与P′重合时，PD+PE=P′E+P′B=BE=2，此时PD+PE的值最小，
所以答案是2．
【考点精析】解答此题的关键在于理解等边三角形的性质的相关知识，掌握等边三角形的三个角都相等并且每个角都是60°，以及对正方形的性质的理解，了解正方形四个角都是直角，四条边都相等；正方形的两条对角线相等，并且互相垂直平分，每条对角线平分一组对角；正方形的一条对角线把正方形分成两个全等的等腰直角三角形；正方形的对角线与边的夹角是45o；正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形．
练习册系列答案
100分闯关期末冲刺系列答案
相关题目
