题目内容
【题目】如图,在![]() 中,∠A=90°,
中,∠A=90°,![]() 是
是![]() 的中点,过点
的中点,过点![]() 的直线
的直线![]() 、
、![]() 交直线
交直线![]() 、
、![]() 于点
于点![]() 、
、![]() ,且
,且![]() ,连接
,连接![]() .
.
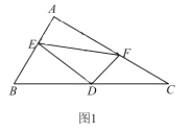
(1)如图1,求证:![]() ;
;
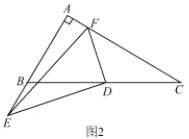
(2)如图2,若![]() ,
,![]() ,
,![]() ,请直接写出线段
,请直接写出线段![]() 的长度.(不必写过程)
的长度.(不必写过程)
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)如图1中,延长ED到H,使得ED=DH,连接FH,CH.想办法证明EF=FH,CH=BE,∠FCH=90°即可解决问题;
(2)如图2中,延长ED到H,使得ED=DH,连接FH,CH.作DK⊥AC于K.,设AC交DH于点O.想办法求出CH的长,利用(1)中结论即可解决问题;
解:(1)如图1中,延长ED到H,使得ED=DH,连接FH,CH.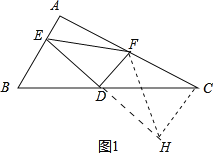
∵BD=DC,DE=DH,∠BDE=∠CDH,
∴△BDE≌△CDH(SAS),
∴BE=CH,∠B=∠DCH,
∵∠A=90°,
∴∠ACB+∠B=∠ACB+∠DCH=90°,
∴∠FCH=90°,
∴FH2=FC2+CH2=FC2+BE2,
∵FD⊥EH,DE=DH,
∴EF=FH,
∴EF2=BE2+CF2;
(2)如图2中,延长ED到H,使得ED=DH,连接FH,CH.作DK⊥AC于K.,设AC交DH于点O.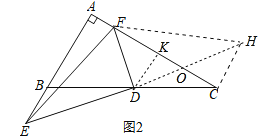
同(1)的方法易证△BDE≌△CDH(SAS),∠FCH=90°,DK∥CH,
∴BE=CH,可得EF2=BE2+CF2,
∵∠A=90°,AB=6,∠ACB=30°,
∴BC=12
∴AC= ![]() ,
,
∵AF=![]() ,
,
∴CF=5![]() ,
,
∵BD=DC,DK∥AB,
∴AK=KC=3![]() ,FK=2
,FK=2![]() ,DK=
,DK=![]() AB=3,
AB=3,
∴DF=![]() ,
,
∵OD⊥DF,DK⊥OF,
∴![]() ,
,![]() ,
,
∴OK=![]() ,
,
∴OC=![]() =
=![]() ,
,
∴OC= OK,
∵DK∥CH,
∴∠ODK=∠OHC,∠OKD=∠OCH,
∴△OHC≌△ODK,
∴CH= DK =3,
∴EF=![]() ,
,

【题目】某宾馆拥有客房100间,经营中发现:每天入住的客房数y(间)与房价x(元)(180≤x≤300)满足一次函数关系,部分对应值如下表:
x(元) | 180 | 260 | 280 | 300 |
y(间) | 100 | 60 | 50 | 40 |
(1)求y与x之间的函数表达式;
(2)已知每间入住的客房,宾馆每日需支出各种费用100元;每间空置的客房,宾馆每日需支出各种费用60元.当房价为多少元时,宾馆当日利润最大?求出最大利润.(宾馆当日利润=当日房费收入-当日支出)