题目内容
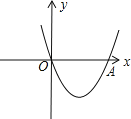
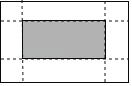
【题目】如图，有一张矩形纸片，长15cm，宽9cm，在它的四角各剪去一个同样的小正方形，然折叠成一个无盖的长方体纸盒．若纸盒的底面（图中阴影部分）面积是48cm2，求剪去的小正方形的边长．设剪去的小正方形边长是xcm，根据题意可列方程为_____．
【答案】（15﹣2x）（9﹣2x）＝48．
【解析】
设剪去的小正方形边长是xcm，则纸盒底面的长为（15﹣2x）cm，宽为（9﹣2x）cm，根据长方形的面积公式结合纸盒的底面（图中阴影部分）面积是48cm2，即可得出关于x的一元二次方程，此题得解．
解：设剪去的小正方形边长是xcm，则纸盒底面的长为（15﹣2x）cm，宽为（9﹣2x）cm，
根据题意得：（15﹣2x）（9﹣2x）＝48．
故答案是：（15﹣2x）（9﹣2x）＝48．
练习册系列答案
相关题目
【题目】二次函数y＝ax2+bx+c（a≠0）中的x与y的部分对应值如下表：
x | … | ﹣3 | ﹣2 | ﹣1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 12 | 5 | 0 | ﹣3 | ﹣4 | ﹣3 | 0 | 5 | … |
给出以下结论：（1）二次函数y＝ax2+bx+c有最小值，最小值为﹣3；（2）当﹣
＜x＜2时，y＜0；（3）已知点A（x1，y1）、B（x2，y2）在函数的图象上，则当﹣1＜x1＜0，3＜x2＜4时，y1＞y2．上述结论中正确的结论个数为（ ）
A.0B.1C.2D.3
