题目内容
【题目】如图,兰博基尼某车型车门设计属于剪刀门设计,即车门关闭时位置如图中四边形ABCD,车门打开是绕点A逆时针旋转至CD与AD垂直,已知四边形ABCD与四边形AB′C′D′在同一平面,若AD∥BC,∠D=45°,∠DAB′=30°,CD=60cm,则AB的长约为( )(![]() ≈1.7)
≈1.7)
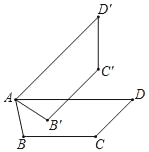
A. 21cmB. 42cmC. 51cmD. 60cm
【答案】B
【解析】
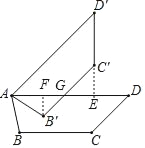
设AD与B′C′交于G,过B′作B′F⊥AD于F,延长D′C′交AD于E,根据旋转的性质得到∠D′=∠D=45°,AB′=AB,C′D′=CD=60cm,根据等腰直角三角形的性质得到C′E=GE,求得AG=C′D′=60,解直角三角形即可得到结论.
解:设AD与B′C′交于G,
过B′作B′F⊥AD于F,延长D′C′交AD于E,
由旋转的性质得,∠D′=∠D=45°,AB′=AB,C′D′=CD=60cm,
∵D′C′⊥AD,
∴∠AED′=90°,
∴△AED′是等腰直角三角形,
∴AE=D′E,
∵AD∥BC,
∴AD′∥B′C′,
∴△GC′E是等腰直角三角形,
∴C′E=GE,
∴AG=C′D′=60,
∵∠FGB′=∠C′GE=45°,
∴FG=FB′,
∵∠DAB′=30°,
∴AF=![]() FB′,
FB′,
∴FB′+![]() FB′=60,
FB′=60,
∴FB′=30(![]() ﹣1),
﹣1),
∴AB=AB′=2FB′=60(![]() ﹣1)=42cm.
﹣1)=42cm.
故选:B.

练习册系列答案
相关题目