题目内容
【题目】在湖边高出水面40m的山顶A处看见一架无人机停留在湖面上空某处,观察到无人机底部标志P处的仰角为45°,又观其在湖中之像的俯角为60°,则无人机底部P距离湖面的高度是( )
A. (40![]() +40)mB. (40
+40)mB. (40![]() +80)mC. (50
+80)mC. (50![]() +100)mD. (50
+100)mD. (50![]() +50)m
+50)m
【答案】B
【解析】
设AE=x,则PE=AE=x,根据山顶A处高出水面40m,得出OE=40,OP′=x+40,根据∠P′AE=60°,得出P′E=![]() x,从而列出方程,求出x的值即可.
x,从而列出方程,求出x的值即可.
解:设AE=xm,
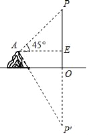
在Rt△AEP中∠PAE=45°,则∠P=45°,
∴PE=AE=x,
∵山顶A处高出水面40m,
∴OE=40m,
∴OP′=OP=PE+OE=x+40,
∵∠P′AE=60°,
∴P′E=tan60°AE=![]() x,
x,
∴OP′=P′E﹣OE=![]() x﹣40,
x﹣40,
∴x+40=![]() x﹣40,
x﹣40,
解得:x=40(![]() +1)(m),
+1)(m),
∴PO=PE+OE=40(![]() +1)+40=40
+1)+40=40![]() +80(m),
+80(m),
即无人机离开湖面的高度是(40![]() +80)m.
+80)m.
故选:B.

练习册系列答案
相关题目