题目内容
【题目】如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:
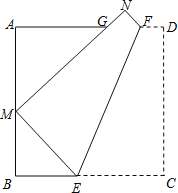
(1)△AGM∽△BME;
(2)若M为AB中点,则![]() =
=![]() =
=![]() ;
;
(3)△AGM的周长为2a.
【答案】见解析
【解析】
试题分析:(1)根据正方形的性质和折叠的性质得出∠A=∠B,∠AGM=∠BME,再利用相似三角形的判定证明即可;
(2)设BE=x,利用勾股定理得出x的值,再利用相似三角形的性质证明即可;
(3)设BM=x,AM=a﹣x,利用勾股定理和相似三角形的性质证明即可.
证明:(1)∵四边形ABCD是正方形,
∴∠A=∠B=∠C=90°,
∴∠AMG+∠AGM=90°,
∵EF为折痕,
∴∠GME=∠C=90°,
∴∠AMG+∠BME=90°,
∴∠AGM=∠BME,
在△AGM与△BME中,
∵∠A=∠B,∠AGM=∠BME,
∴△AGM∽△BME;
(2)∵M为AB中点,
∴BM=AM=![]() ,
,
设BE=x,则ME=CE=a﹣x,
在Rt△BME中,∠B=90°,
∴BM2+BE2=ME2,即(![]() )2+x2=(a﹣x)2,
)2+x2=(a﹣x)2,
∴x=![]() a,
a,
∴BE=![]() a,ME=
a,ME=![]() a,
a,
由(1)知,△AGM∽△BME,
∴![]() =
=![]() =
=![]() =
=![]() ,
,
∴AG=![]() BM=
BM=![]() a,GM=
a,GM=![]() ME=
ME=![]() a,
a,
∴![]() =
=![]() =
=![]() ;
;
(3)设BM=x,则AM=a﹣x,ME=CE=a﹣BE,
在Rt△BME中,∠B=90°,
∴BM2+BE2=ME2,即x2+BE2=(a﹣BE)2,
解得:BE=![]() ﹣
﹣![]() ,
,
由(1)知,△AGM∽△BME,
∴![]() =
=![]() =
=![]() ,
,
∵C△BME=BM+BE+ME=BM+BE+CE=BM+BC=a+x,
∴C△AGM=C△BME![]() =(a+x)
=(a+x)![]() =2a.
=2a.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目

