��Ŀ����
����Ŀ����OΪֱ��AB��һ�㣬��ֱ��ABͬ����������OC��OD��ʹ�á�COD=90��
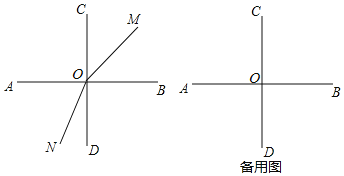
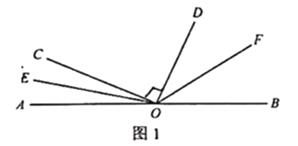
��1����ͼ1������O������OE����OEǡ��Ϊ��AOC�Ľ�ƽ����ʱ����������OF��ʹ��OFƽ�֡�BOD�����EOF�Ķ�����__________�ȣ�
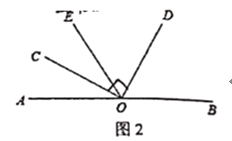
��2����ͼ2������O������OE����OEǡ��Ϊ��AOD�Ľ�ƽ����ʱ�������BOD���COE��������ϵ��
��3������O������OE����OCǡ��Ϊ��AOE�Ľ�ƽ����ʱ����������OF��ʹ��OFƽ�֡�COD������EOC=3��EOF��ֱ��д����AOE�Ķ���
���𰸡���1��135�㣻��2����BOD=2��COE����3��67.5��.
��������
��1���ɡ�COD=90�������AOC+��BOD=90�㣬��OEƽ�֡�AOC��OFƽ�֡�BOD���á�COE+��DOF=45�㣬���������EOF�Ķ�����
��2��������ó���BOD+��AOC=90������BOD=180��![]() ��AOD�����ɽ�ƽ���ߵĶ�����м��㣬���ɵó������
��AOD�����ɽ�ƽ���ߵĶ�����м��㣬���ɵó������
��3���ɽ�ƽ���߶���ó���AOC=��COE����COF=��DOF=45�������ɡ�BOD+��AOC=90�������EOF=x�����EOC=3x����COF=4x����������ó����̣��ⷽ�̼��ɣ�
�⣺��1����ͼ��
�ߡ�COD=90�㣬
���AOC+��BOD=90�㣬
��OEƽ�֡�AOC��OFƽ�֡�BOD��
���COE+��DOF=![]() ��
��
���EOF=��COE+��COD+��DOF=45��+90��=135�㣻
�ʴ�Ϊ��135�㣻
��2����BOD=2��COE��
�������£���ͼ��
�ߡ�COD=90����
���BOD+��AOC=90����
��OEƽ�֡�AOD��
���AOE=��DOE=![]() ��AOD��
��AOD��
�֡ߡ�BOD=180��![]() ��AOD��
��AOD��
���COE=��AOE![]() ��AOC
��AOC
=![]() ��AOD
��AOD![]() ��90��
��90��![]() ��BOD��
��BOD��
=![]() ��180��
��180��![]() ��BOD��
��BOD��![]() 90��+��BOD
90��+��BOD
=![]() ��BOD��
��BOD��
���BOD=2��COE��
��3����ͼ��
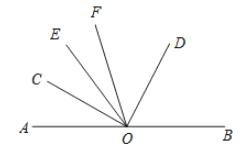
��OCΪ��AOE�Ľ�ƽ���ߣ�OFƽ�֡�COD��
���AOC=��COE����COF=��DOF=45����
�ߡ�EOC=3��EOF��
���EOF=x�����EOC=3x��
���COF=4x��
���AOE=2��COE=6x����DOF=4x��
�ߡ�COD=90����
��4x+4x=90����
��ã�x=11.25����
���AOE=6��11.25��=67.5����

 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�