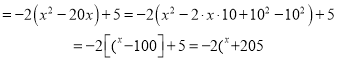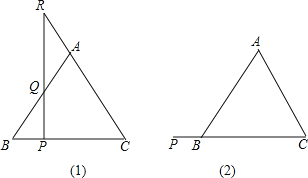题目内容
【题目】(1)如图,在△ABC中,∠ABC、∠ACB的平分线相交于F,过F作DE∥BC,分别交AB、AC于点D、E.判断DE=DB+EC是否成立?为什么?

(2)如图,若点F是∠ABC的平分线和外角∠ACG的平分线的交点,其他条件不变,请猜想线段DE、DB、EC之间有何数量关系?
证明你的猜想。

【答案】(1)成立,证明见解析.(2)证明见解析.
【解析】试题分析: ![]() 根据平行线的性质和角平分线的性质,得出
根据平行线的性质和角平分线的性质,得出![]() 和
和![]() 是等腰三角形,通过等量代换即可得出结论.
是等腰三角形,通过等量代换即可得出结论.
![]() 同
同![]() ,只要求出
,只要求出![]() 和
和![]() 是等腰三角形即可.
是等腰三角形即可.
试题解析:(1)成立;
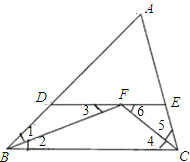
∵△ABC中BF、CF平分∠ABC、∠ACB,
∴∠1=∠2,∠5=∠4.
∵DE∥BC,∴∠2=∠3,∠4=∠6.
∴∠1=∠3,∠6=∠5.
根据在同一个三角形中,等角对等边的性质,可知:BD=DF,EF=CE.
∴DE=DF+EF=BD+CE.
故成立.
(2)∵BF分∠ABC,
∴∠DBF=∠FBC.
![]()
∴∠DFB=∠FBC.
∴∠ABF=∠DFB,
∴BD=DF.
∵CF平分∠ACG,
∴∠ACF=∠FCG.
![]()
∴∠DFC=∠FCG.
∴∠ACF=∠DFC,
∴CE=EF.
∴EF+DE=DF,即DE+EC=BD.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目