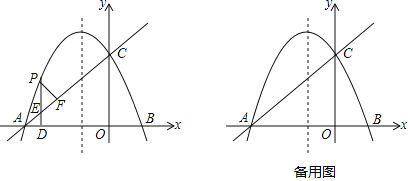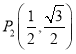题目内容
【题目】有这样一个问题：探究方程x3﹣x﹣2＝0的实数根的个数.
小芳想起了曾经解决的一个问题：通过函数图象探究方程x2+3x﹣1＝0的实数根的个数，她想到了如下的几个方法：
方法1：方程x2+3x﹣1＝0的根可以看作是抛物线y＝x2+3x﹣1与直线y＝0（即x轴）交点的横坐标；这两个图象的交点个数即是方程x2+3x﹣1＝0的实数根的个数.
方法2：将方程变形成x2＝﹣3x+1，那么方程x2+3x﹣1＝0的根也可以看作是抛物线y＝x2与直线y＝﹣3x+1交点的横坐标；这两个图象的交点个数即是方程x2+3x﹣1＝0的实数根的个数.
方法3：由于x≠0，将方程变形成
，那么方程x2+3x﹣1＝0的根也可以看作是直线y＝x+3与双曲线
交点的横坐标；这两个图象的交点个数即是方程x2+3x﹣1＝0的实数根的个数.
她类比上述方法，借助函数图象的交点个数对方程x3﹣x﹣2＝0的实数根的个数进行了探究.
下面是小芳的探究过程，请补充完成：
（1）x＝0 方程x3﹣x﹣2＝0的根；（填”是”或”不是”）
（2）方程x3﹣x﹣2＝0的根可以看作是函数 与函数 的图象交点的横坐标；
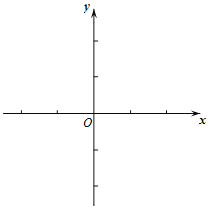
（3）在同一坐标系中画出两个函数的图象；
（4）观察图象可得，方程x3﹣x﹣2＝0的实数根的个数是 个.
【答案】（1）不是；（2）y＝x2﹣1， 
；（3）见解析；（4）1
【解析】
（1）将x＝0代入x3﹣x﹣2中，可知x＝0不是方程x3﹣x﹣2＝0的根；
（2）将原方程变形为
（x≠0），由此即可得出结论；
（3）画出函数y＝x2﹣1与函数的图象；
（4）根据两函数图象交点的个数，找出方程解得个数.
解：（1）当x＝0时，x3﹣x﹣2＝﹣2，
∴x＝0不是方程x3﹣x﹣2＝0的根.
故答案为：不是.
（2）∵方程x3﹣x﹣2＝0可变形为（x≠0），
∴方程x3﹣x﹣2＝0的根可以看作是函数y＝x2﹣1与函数的图象交点的横坐标.
故答案为：y＝x2﹣1；.
（3）画出两函数图象，如图所示.
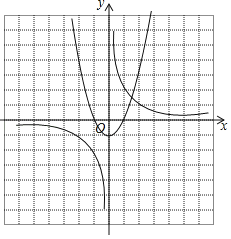
（4）观察图象可知，函数y＝x2﹣1与函数的图象只有一个交点，
∴方程x3﹣x﹣2＝0的实数根的个数是1个.
故答案为：1.
【题目】某校为了解学生每月零用钱情况，从七、八、九年级1200名学生中随机抽取部分学生，对他们今年4月份的零用钱支出情况进行调查统计并绘制成如下统计图表：
组别 | 零用钱支出x（单位：元） | 频数（人数） | 频率 |
节俭型 | x＜10 | 2 | 0.05 |
10≤x＜20 | 4 | 0.10 | |
富足型 | 20≤x＜30 | 12 | |
30≤x＜40 | m | ||
奢侈型 | 40≤x＜50 | n | |
x≥50 | 2 |
请根据图表中所给的信息，解答下列问题：
（1）在这次调查中共随机抽取了 名学生，图表中的m＝ ，n＝ ；
（2）请估计该校今年4月份零用钱支出在“30≤x＜40范围的学生人数；
（3）在抽样的“节俭型”学生中，有2位男生和4位女生，校团委计划从中随机抽取两人参与“映山红”的公益活动，求恰好抽中一男一女的概率．
