题目内容
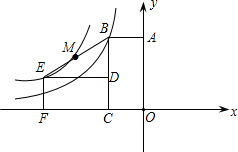
如图,已知矩形ABCD的边BC在x轴上,矩形ABCD对角线的交点E的横坐标为m(m>0),且点A、E 和点N(1,2)都在函数y=
和点N(1,2)都在函数y=
的图象上.
(1)求k的值;
(2)求点A的坐标(用m表示);
(3)当满足上述条件的矩形ABCD为正方形时,请求出此时m的值;
(4)点F在y轴的正半轴上,且OF=OB,在(3)的条件下,是否线段BC上存在点P,使PD=PF,若存在,求出符合条件的点P的坐标,若不存在,请说明理由.
 和点N(1,2)都在函数y=
和点N(1,2)都在函数y=| k |
| x |
(1)求k的值;
(2)求点A的坐标(用m表示);
(3)当满足上述条件的矩形ABCD为正方形时,请求出此时m的值;
(4)点F在y轴的正半轴上,且OF=OB,在(3)的条件下,是否线段BC上存在点P,使PD=PF,若存在,求出符合条件的点P的坐标,若不存在,请说明理由.
(1)因为抛物线过N(1,2),所以k=2;
(2)∵E的横坐标为m(m>0),
∴纵坐标为
,根据矩形性质,AB=
,即A点纵坐标为
,代入y=
中,得x=
,
∴A(
,
);
(3)根据上面的解题过程可得B(
,0),C(
m,0),BC=m,
∵AB=BC,∴
=m,解得m=±2,
∵m>0,∴m=2;
(4)若PD=PF,则P为DF的垂直平分线与x轴的交点,
根据题意在BC上,设其坐标为P(x,0),则PC=3-x,
根据勾股定理得
=
,解得x=2,
∴线段BC上存在点P,使PD=PF,P(2,0).

(2)∵E的横坐标为m(m>0),
∴纵坐标为
| 2 |
| m |
| 4 |
| m |
| 4 |
| m |
| 2 |
| x |
| m |
| 2 |
∴A(
| m |
| 2 |
| 4 |
| m |
(3)根据上面的解题过程可得B(
| m |
| 2 |
| 3 |
| 2 |
∵AB=BC,∴
| 4 |
| m |
∵m>0,∴m=2;
(4)若PD=PF,则P为DF的垂直平分线与x轴的交点,
根据题意在BC上,设其坐标为P(x,0),则PC=3-x,
根据勾股定理得
| x2+12 |
| (3-x)2+22 |
∴线段BC上存在点P,使PD=PF,P(2,0).


练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目



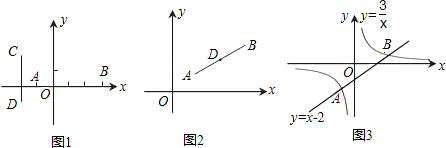
 点A的横坐标为2,过点A作AB⊥x轴于点B,且S△ABC:S△ABO=4:1.
点A的横坐标为2,过点A作AB⊥x轴于点B,且S△ABC:S△ABO=4:1.