题目内容
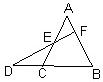16、如图，已知D是△ABC的边BC延长线上一点，DF⊥AB于点F，交AC于点E，∠A=40°，∠D=30°，则∠ACB的度数80
度．分析：在直角三角形DFB中，根据三角形内角和定理，求得∠B的度数；再在△ABC中求∠ACB的度数即可．
解答：解：在△DFB中，
∵DF⊥AB，
∴∠DFB=90°，
∵∠D=30°，∠DFB+∠D+∠B=180°，
∴∠B=60°．
在△ABC中，
∠A=40°，∠B=60°，
∴∠ACB=180°-∠A-∠B=80°．
所以∠ACB的度数是80度．
∵DF⊥AB，
∴∠DFB=90°，
∵∠D=30°，∠DFB+∠D+∠B=180°，
∴∠B=60°．
在△ABC中，
∠A=40°，∠B=60°，
∴∠ACB=180°-∠A-∠B=80°．
所以∠ACB的度数是80度．
点评：解答本题时，主要利用了三角形内角和定理．
练习册系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
16、如图，已知O是AB的中点，再加上什么条件，能使△AOC和△BOD全等？为什么？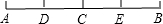
如图，已知M是AB的中点，N是AC的中点，若MN=5cm，则BC=
如图，已知M是AB的中点，AC∥MD，AC=MD，试说明下面结论成立的理由：（1）△ACM≌△MDB；（2）CM=DB，CM∥DB．
如图，已知M是AB的中点，下面哪个结论不是根据“M是AB的中点”推出来的（ ）