题目内容
如图,已知C是AB的中点,D是AC的中点,E是BC的中点.(1)若DE=9cm,求AB的长;
(2)若CE=5cm,求DB的长.
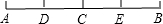
分析:(1)根据中点的概念,可以证明:AB=2DE,故AB的长可求;
(2)由CE的长先求得BC的长,再根据C是AB的中点,D是AC的中点求得CD的长,最后即可求得BD的长.
(2)由CE的长先求得BC的长,再根据C是AB的中点,D是AC的中点求得CD的长,最后即可求得BD的长.
解答:解:(1)∵D是AC的中点,E是BC的中点,
∴AC=2CD,BC=2CE,
∴AB=AC+BC=2DE=18cm;
(2)∵E是BC的中点,
∴BC=2CE=10cm,
∵C是AB的中点,D是AC的中点,
∴DC=
AC=
BC=5cm,
∴DB=DC+CB=10+5=15cm.
∴AC=2CD,BC=2CE,
∴AB=AC+BC=2DE=18cm;
(2)∵E是BC的中点,
∴BC=2CE=10cm,
∵C是AB的中点,D是AC的中点,
∴DC=
| 1 |
| 2 |
| 1 |
| 2 |
∴DB=DC+CB=10+5=15cm.
点评:考查了线段的中点的概念.利用中点性质转化线段之间的倍分关系是解题的关键,灵活运用线段的和、差、倍、分转化线段之间的数量关系也是十分关键的一点.

练习册系列答案
相关题目
 16、如图,已知O是AB的中点,再加上什么条件,能使△AOC和△BOD全等?为什么?
16、如图,已知O是AB的中点,再加上什么条件,能使△AOC和△BOD全等?为什么? 如图,已知M是AB的中点,N是AC的中点,若MN=5cm,则BC=
如图,已知M是AB的中点,N是AC的中点,若MN=5cm,则BC= 如图,已知CD是AB的中垂线,垂足为点D,DE⊥AC于点E,DF⊥BC于点F.
如图,已知CD是AB的中垂线,垂足为点D,DE⊥AC于点E,DF⊥BC于点F. 如图,已知M是AB的中点,AC∥MD,AC=MD,试说明下面结论成立的理由:(1)△ACM≌△MDB;(2)CM=DB,CM∥DB.
如图,已知M是AB的中点,AC∥MD,AC=MD,试说明下面结论成立的理由:(1)△ACM≌△MDB;(2)CM=DB,CM∥DB.