题目内容
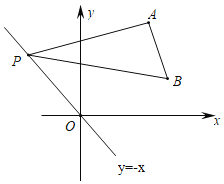
【题目】如图,已知直线y=![]() x+2与x轴、y轴分别交于点B,C,抛物线y=
x+2与x轴、y轴分别交于点B,C,抛物线y=![]() x2+bx+c过点B、C,且与x轴交于另一个点A.
x2+bx+c过点B、C,且与x轴交于另一个点A.
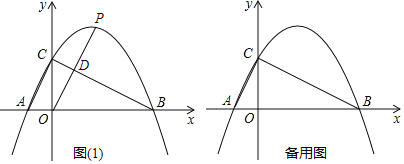
(1)求该抛物线的表达式;
(2)若点P是x轴上方抛物线上一点,连接OP.
①若OP与线段BC交于点D,则当D为OP中点时,求出点P坐标.
②在抛物线上是否存在点P,使得∠POC=∠ACO若存在,求出点P坐标;若不存在,请说明理由.
【答案】(1)y=﹣![]() x2+
x2+![]() x+2;(2)①点P坐标为(2,3);②存在点P(
x+2;(2)①点P坐标为(2,3);②存在点P(![]() ,
,![]() ﹣1)或(
﹣1)或(![]() ,
,![]() ﹣7)使得∠POC=∠ACO
﹣7)使得∠POC=∠ACO
【解析】
(1)![]() 与x轴、y轴分别交于点B(4,0)、C(0,2),由题意可得
与x轴、y轴分别交于点B(4,0)、C(0,2),由题意可得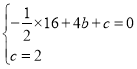 即可求解;
即可求解;
(2)①过点P作PE∥OC,交BC于点E.根据题意得出△OCD≌△PED,从而得出PE=OC=2,再根据 ![]() 即可求解;
即可求解;
②当点P在y轴右侧,PO∥AC时,∠POC=∠ACO.抛物线与x轴交于A,B两点,点A在点B左侧,则点A坐标为(-1,0).则直线AC的解析式为y=2x+2.直线OP的解析式为y=2x,即可求解;当点P在y轴右侧,设OP与直线AC交于点G,当CG=OG时,∠POC=∠ACO,根据等腰三角形三线合一,则CF=OF=1,可得:点G坐标为![]() 即可求解.
即可求解.
(1)∵y=﹣![]() x+2与x轴、y轴分别交于点B(4,0)、C(0,2).
x+2与x轴、y轴分别交于点B(4,0)、C(0,2).
由题意可得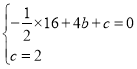 ,解得:
,解得:![]() ,
,
∴抛物线的表达式为y=﹣![]() x2+
x2+![]() x+2;
x+2;
(2)①如图,过点P作PE∥OC,交BC于点E.
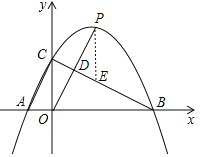
∵点D为OP的中点,
∴△OCD≌△PED(AAS),
∴PE=OC=2,
设点P坐标为(m,﹣![]() m2+
m2+![]() m+2),点E坐标为(m,﹣
m+2),点E坐标为(m,﹣![]() m+2),
m+2),
则PE=(﹣![]() m2+
m2+![]() m+2)﹣(﹣
m+2)﹣(﹣![]() m+2)=﹣
m+2)=﹣![]() m2+2m=2,
m2+2m=2,
解得m1=m2=2.
∴点P坐标为(2,3);
②存在点P,使得∠POC=∠ACO.
理由:分两种情况讨论.
如上图,当点P在y轴右侧,
PO∥AC时,∠POC=∠ACO.
∵抛物线与x轴交于A,B两点,点A在点B左侧,
∴点A坐标为(﹣1,0).
∴直线AC的解析式为y=2x+2.
∴直线OP的解析式为y=2x,
解方程组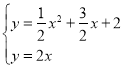 ,解得:x=
,解得:x=![]() (舍去负值)
(舍去负值)
∴点P坐标为(![]() ,
,![]() ﹣1).
﹣1).
如图,当点P在y轴右侧,
设OP与直线AC交于点G,当CG=OG时∠POC=∠ACO,
过点G作GF⊥OC,垂足为F.
根据等腰三角形三线合一,则CF=OF=1.
∴可得点G坐标为(﹣![]() ,1)
,1)
∴直线OG的解析式为y=﹣2x;
把y=﹣2x代入抛物线表达式并解得x=![]() (不合题意值已舍去).
(不合题意值已舍去).
∴点P坐标为(![]() ,
,![]() ﹣7).
﹣7).
综上所述,存在点P(![]() ,
,![]() ﹣1)或(
﹣1)或(![]() ,
,![]() ﹣7)使得∠POC=∠ACO.
﹣7)使得∠POC=∠ACO.

 科学实验活动册系列答案
科学实验活动册系列答案