��Ŀ����
��ֱ������ϵxOy�У���֪������y=ax2+bx+c�Ŀ������ϣ�����P��ֱ��y=-4x�ϣ���P������ԭ�����Ϊ| 17 |
��1����������ߵĽ���ʽ��
��2����Q��������������A��B��P�ĵ㣬�ҡ�QAP=90�㣬���Q�����꣮�����á�������ľ���ֵ�����߶γ�����ͨ�����뼸�Σ�ת��Ϊ�������ú���֪ʶ��ת��Ϊ�߶γ��ü���֪ʶ��
��������1���ɶ���P��ֱ��y=-4x�ϣ���P������ԭ�����Ϊ
���ɵó���P�����꣬�����ù��ɶ������Խ����
��2���������Q�����꣬��ʾ��AQ��QP�ij��ȣ����ù��ɶ������Խ����
| 17 |
��2���������Q�����꣬��ʾ��AQ��QP�ij��ȣ����ù��ɶ������Խ����
����⣺��1���߶���P��ֱ��y=-4x�ϣ�
����P��a1��-4a��������a2+(-4a)2=(
)2��
��ã�a=��1��
��P��1��-4����-1��4����
�������߿������ϣ�����x���н��㣬
�ࣨ-1��4������������ȥ��
��y=a��x-1��2-4=ax2-2ax+a-4��x�ύ�ڵ�A��x1��0����
B��{x2��0��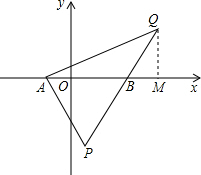 ��
��
��
��x1��x2��
���a=1��
��2����ͼ��ʾ�����������ϵ�Q��m��n������Q��QM��x���ڵ�M��
AQ=
��QP=
��
AP=2
��
�ߡ�QAP=90�㣬�ɹ��ɶ�������(
)2+(2
)2=��m-1��2+��n+4��2��
��������m-2n+1=0����n=m2-2m-3��
���
������������ȥ����
��
��Q��
��
����
����P��a1��-4a��������a2+(-4a)2=(
| 17 |
��ã�a=��1��
��P��1��-4����-1��4����
�������߿������ϣ�����x���н��㣬
�ࣨ-1��4������������ȥ��
��y=a��x-1��2-4=ax2-2ax+a-4��x�ύ�ڵ�A��x1��0����
B��{x2��0��
 ��
��
|
��x1��x2��
���a=1��
��2����ͼ��ʾ�����������ϵ�Q��m��n������Q��QM��x���ڵ�M��
AQ=
| (m+1)2+n2 |
| (m-1)2+(n+4)2 |
AP=2
| 5 |
�ߡ�QAP=90�㣬�ɹ��ɶ�������(
| (m+1)2+n2 |
| 5 |
��������m-2n+1=0����n=m2-2m-3��
���
|
|
��Q��
| 7 |
| 2 |
| 9 |
| 4 |
������������Ҫ�����˶��κ�����һ�κ����ۺ�Ӧ�ã��Լ����ɶ�����Ӧ�ã��������ϴ�Ӧ������㣮

��ϰ��ϵ�д�
 ���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д�
���Ͱ�ͨ�������Сѧ��ʱͬ�����ϵ�д� ���Ͱ�ͨ������ϵ�д�
���Ͱ�ͨ������ϵ�д� �ٷ�ѧ����ҵ��������ϵ�д�
�ٷ�ѧ����ҵ��������ϵ�д�
�����Ŀ

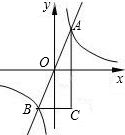 ��ֱ������ϵxoy�У�����y=4x��ͼ���뷴��������y=
��ֱ������ϵxoy�У�����y=4x��ͼ���뷴��������y= ��2012•������ģ����֪����ͼ����ֱ������ϵxOy�У���A��8��0����B��0��6������C��x��ĸ������ϣ�AB=AC������M��x���ϴӵ�C���A�ƶ�������N���߶�AB�ϴӵ�A���B�ƶ�����M��Nͬʱ���������ƶ����ٶȶ�Ϊÿ��1����λ���ƶ�ʱ��Ϊt�루0��t��10����
��2012•������ģ����֪����ͼ����ֱ������ϵxOy�У���A��8��0����B��0��6������C��x��ĸ������ϣ�AB=AC������M��x���ϴӵ�C���A�ƶ�������N���߶�AB�ϴӵ�A���B�ƶ�����M��Nͬʱ���������ƶ����ٶȶ�Ϊÿ��1����λ���ƶ�ʱ��Ϊt�루0��t��10���� ��ʽΪy=x2-mx+n������x2-mx+n=0������������Ϊ-4��
��ʽΪy=x2-mx+n������x2-mx+n=0������������Ϊ-4��