题目内容
首先,我们看两个问题的解答:问题1:已知x>0,求x+
| 3 |
| x |
问题2:已知t>2,求
| t2-5t+9 |
| t-2 |
问题1解答:对于x>0,我们有:x+
| 3 |
| x |
| x |
| ||
|
| 3 |
| 3 |
| x |
| ||
|
| 3 |
| 3 |
| x |
| 3 |
问题2解答:令x=t-2,则t=x+2,于是
| t2-5t+9 |
| t-2 |
| (x+2)2-5(x+2)+9 |
| x |
| x2-x+3 |
| x |
| 3 |
| x |
由问题1的解答知,x+
| 3 |
| x |
| 3 |
| t2-5t+9 |
| t-2 |
| 3 |
弄清上述问题及解答方法之后,解答下述问题:
在直角坐标系xOy中,一次函数y=kx+b(k>0,b>0)的图象与x轴、y轴分别交于A、B两点,且使得△OAB的面积值等于|OA|+|OB|+3.
(1)用b表示k;
(2)求△AOB面积的最小值.
分析:(1)用k和b表示出三角形的直角边的长,从而表示出面积,和△OAB的面积值等于|OA|+|OB|+3列成方程,用b表示k.
(2)设x=b-2,则b=x+2,根据题干中第二问所给的解答过程得到提示,配方后求得x成立时的最小值.
(2)设x=b-2,则b=x+2,根据题干中第二问所给的解答过程得到提示,配方后求得x成立时的最小值.
解答:解:(1)当x=0时,y=b;当y=0时,x=-
.
所以|OA|=
,|OB|=b.
∴S△OAB=
|OA|•|OB|=
.
∴
=
+b+3,
∴
=b+3,k=
.
(2)S△OAB=
=
=
.
设x=b-2,则b=x+2.
S△OAB=
=
=x+
+7
=(
-
)2+7+2
≥7+2
.
上述不等式等号在x=
时成立.
故△OAB面积最小值是7+2
.
| b |
| k |
所以|OA|=
| b |
| k |
∴S△OAB=
| 1 |
| 2 |
| b2 |
| 2k |
∴
| b2 |
| 2k |
| b |
| k |
∴
| b2-2b |
| 2k |
| b2-2b |
| 2b+6 |
(2)S△OAB=
| b2 |
| 2k |
| b2(2b+6) |
| 2(b2-2b) |
| b2+3b |
| b-2 |
设x=b-2,则b=x+2.
S△OAB=
| (x+2)2+3(x+2) |
| x |
=
| x2+7x+10 |
| x |
=x+
| 10 |
| x |
=(
| x |
|
| 10 |
| 10 |
上述不等式等号在x=
| 10 |
故△OAB面积最小值是7+2
| 10 |
点评:本题考查一次函数的综合运用,以及活学活用的能力,和配方法求最值的情况.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
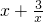 的最小值.
的最小值.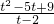 的最小值.
的最小值.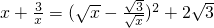 ≥
≥ .当
.当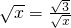 ,即
,即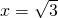 时,上述不等式取等号,所以
时,上述不等式取等号,所以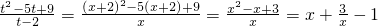 .
.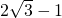 .
. 的最小值.
的最小值. 的最小值.
的最小值. ≥
≥ .当
.当 ,即
,即 时,上述不等式取等号,所以
时,上述不等式取等号,所以 的最小值
的最小值 .
. .
. 的最小值
的最小值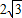 ,所以
,所以 的最小值是
的最小值是 .
.