题目内容
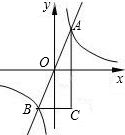 在直角坐标系xoy中,函数y=4x的图象与反比例函数y=
在直角坐标系xoy中,函数y=4x的图象与反比例函数y=| k | x |
(1)求点C的坐标;
(2)求△ABC的面积.
分析:(1)根据函数的图象的特点可知点A、点B关于原点对称,先求出点B的坐标为(-1,4);根据题意可知:点C的横坐标与点A的横坐标相等;点C的纵坐标与点B的纵坐标相等,所以可得点C的坐标为(1,-4).
(2)根据两点距离公式求出三角形的边长,直接利用直角三角形的面积求法计算即可.
(2)根据两点距离公式求出三角形的边长,直接利用直角三角形的面积求法计算即可.
解答:解:(1)因点A的纵坐标为4,故可设点A的坐标为(a,4).
由点A在函数y=4x的图象上,得4=4a,
解得a=1,
于是得点A的坐标为(1,4).
依据反比例函数、正比例函数的对称性,知点A、点B关于原点对称,
故可知点B的坐标为(-1,-4),
又BC与x轴平行,AC与y轴平行,且点C在第四象限,
所以点C的横坐标与点A的横坐标相等;
点C的纵坐标与点B的纵坐标相等,得点C的坐标为(1,-4).
(2)在Rt△ABC中,∠C=90,BC=-|-1-1|=2,AC=|4-(-4)|=8,
所以S△ABC=
BC•AC=
×2×8=8.
答:△ABC的面积为8.
由点A在函数y=4x的图象上,得4=4a,
解得a=1,
于是得点A的坐标为(1,4).
依据反比例函数、正比例函数的对称性,知点A、点B关于原点对称,
故可知点B的坐标为(-1,-4),
又BC与x轴平行,AC与y轴平行,且点C在第四象限,
所以点C的横坐标与点A的横坐标相等;
点C的纵坐标与点B的纵坐标相等,得点C的坐标为(1,-4).
(2)在Rt△ABC中,∠C=90,BC=-|-1-1|=2,AC=|4-(-4)|=8,
所以S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
答:△ABC的面积为8.
点评:主要考查了反比例函数y=
中k的几何意义,即过双曲线上任意一点引x轴、y轴垂线,所得矩形面积为|k|,是经常考查的一个知识点;这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.图象上的点与原点所连的线段、坐标轴、向坐标轴作垂线所围成的直角三角形面积S的关系即S=
|k|.
| k |
| x |
| 1 |
| 2 |

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目

 (2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10).
(2012•北京二模)已知:如图,在直角坐标系xOy中,点A(8,0)、B(0,6),点C在x轴的负半轴上,AB=AC.动点M在x轴上从点C向点A移动,动点N在线段AB上从点A向点B移动,点M、N同时出发,且移动的速度都为每秒1个单位,移动时间为t秒(0<t<10). 析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.
析式为y=x2-mx+n.方程x2-mx+n=0的两根倒数和为-4.