题目内容
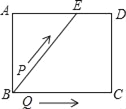
【题目】如图所示,![]() 是等腰直角三角形,
是等腰直角三角形,![]() ,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点O,求证:
,AD是BC边上的中线,过C作AD的垂线,交AB于点E,交AD于点O,求证:![]() .
.

【答案】详见解析
【解析】
∠ADC和∠BDE所在的三角形肯定不全等,那么本题需要作辅助线.△ABC是等腰直角三角形,常用的辅助线是作三线里面的一线.可发现要证全等,已包含两个条件需利用全等得到另一边对应相等.
证明:如图: 作CH⊥AB于H交AD于P,
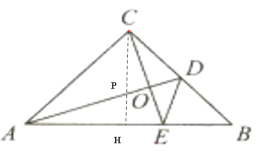
∵在Rt△ABC中,AC=CB,∠ACB=90°,
∴∠CAB=∠CBA=45°.
∴∠HCB=90°-∠CBA=45°=∠CBA=45°.
又∵BC中点为D,
∴CD=BD.
又CH⊥AB,
∴CH=AH=BH.
又∵∠PAH+∠APH=90°,∠PCO+∠CPO=90°,∠APH=∠CPO
∴∠PAH=∠ECH,
在△APH与△CEH中有:
∠PAH=∠ECH,AH=CH,∠PHA=∠EHC,
∴△APH≌△CEH(ASA).
∴PH=EH,
又PC=CH-PH,BE=BH-HE,
∴CP=EB.
∵△ACB是等腰直角三角形,
∴∠B=45°,即∠EBD=45°,CH⊥AB,
∴∠PCD=45°=∠EBD,
在△PDC与△EDB中有:
PC=EB,∠PCD=∠EBD,DC=DB,
∴△PDC≌△EDB(SAS).
∴∠ADC=∠EDB.

练习册系列答案
相关题目
【题目】八(1)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表:
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.