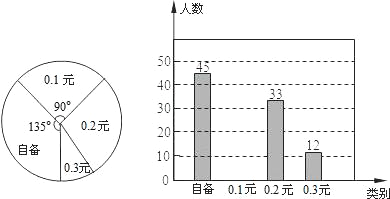
题目内容
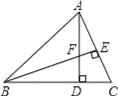
【题目】如图,在△ABC中,AD⊥BC,BE⊥AC,垂足分别为D,E,AD与BE相交于点F.
(1)求证:△ACD∽△BFD;
(2)当tan∠ABD=1,AC=3时,求BF的长.
【答案】(1)证明见解析;(2)3.
【解析】试题分析:(1)、根据双垂直得出∠DBF=∠DAC,然后根据直角得出三角形相似;(2)、根据tan∠ABD=1,∠ADB=90°得出AD=BD,然后根据△ACD和△BFD相似得出BF=AC=3.
试题解析:(1)、∵AD⊥BC,BE⊥AC, ∴∠BDF=∠ADC=∠BEC=90°, ∴∠C+∠DBF=90°,∠C+∠DAC=90°,
∴∠DBF=∠DAC, ∴△ACD∽△BFD.
(2)、∵tan∠ABD=1,∠ADB=90° ∴![]() =1, ∴AD=BD, ∵△ACD∽△BFD, ∴
=1, ∴AD=BD, ∵△ACD∽△BFD, ∴![]() =
=![]() =1, ∴BF=AC=3
=1, ∴BF=AC=3

练习册系列答案
相关题目