题目内容
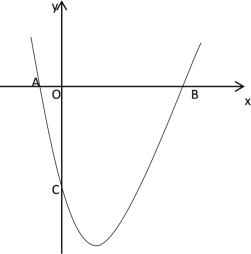
【题目】如图：已知抛物线
与
轴，
轴分别交于点
，此抛物线的对称轴为直线
．
求出此抛物线的解析式；
如图 1，抛物线的顶点为点
，点
是直线
下方抛物线上的一点（异于点），当
时，求出点的坐标；
在的条件下，将抛物线沿射线
方向平移，点的对应点为
，在抛物线平移的过程中，若
，请直接写出此时平移后的抛物线解析式
【答案】（1）
；（2）
；
新抛物线解析式为新抛物线解析式为
或
．
【解析】
（1）根据抛物线的对称轴和A、C两点的坐标即可求出结论；
（2）先求出点D的坐标，过点
作直线
交抛物线于点
，根据平行线的距离处处相等可得此时
，利用待定系数法求出直线BC的解析式，然后求出直线DP的解析式，然后联立方程即可求出点P的坐标；
（3）根据点P′与BC的位置关系分类讨论，分别画出对应的图形，利用待定系数法求出各个直线的解析式，联立方程即可求出点P′的坐标，从而求出平移方式，然后即可求出新抛物线的解析式．
由题抛物线对称轴为直线 
且过点
得
，
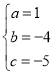
抛物线解析式为
由题抛物线的顶点
过点作直线交抛物线于点，根据平行线的距离处处相等可得此时
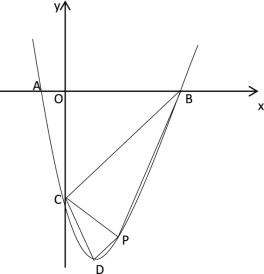
利用对称性可知点B的坐标为（5,0）
设直线BC的解析式为y=kx＋d
将
代入，得
解得：
设直线DP的解析式为y=x＋e
将点D的坐标代入，得
解得：e=-11
则
解得：
（舍去），
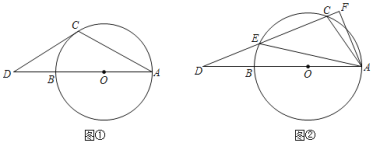
若点P′在BC右侧时，作∠ECB=∠PBC交BP与点E，过点P作PP′∥DC交EC于P′，连接OE，如下图所示，易知点P′符合条件
∴EB=EC
∵OB=OC=5，
∴OE垂直平分BC
∴∠BOE=
∠BOC=45°，即点E在∠BOC的角平分线上
∴可设E点的坐标为（m，-m）
设直线BP的解析式为y=k1x＋b1
将点B、P的坐标代入，可得
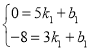
解得：
∴直线BP的解析式为y=4x-20
将点E的坐标代入可得-m=4m-20
解得：m=4
∴点E的坐标为（4，-4）
同理可得CE的解析式为y=
x-5
直线CD的解析式为y=-2x-5
直线PP′的解析式为y=-2x-2
联立
解得：
∴点P′（
）
∴点到点P′（）的平移方式为先向左平移
个单位长度，在向上平移
个单位长度
原抛物线的解析式为
∴新抛物线解析式为
若点P′在BC左侧时，作CP′∥BP，PP′∥CD，CP′与PP′交于点P′，如下图所示，此时
由上可知：直线BP的解析式为y=4x-20，可得直线CP′的解析式为y=4x-5
直线PP′的解析式为y=-2x-2
联立
解得：
∴点P′（
）
∴点到点P′（）的平移方式为先向左平移
个单位长度，在向上平移5个单位长度
原抛物线的解析式为
∴新抛物线解析式为
综上：新抛物线解析式为或
