题目内容
若a、b、c、d是互不相等的整数（a＜b＜c＜d），且abcd=121，则ac+bd=
-12
-12
．分析：由已知四个整数a，b，c，d的积等于121，又121=11×11，所以只存在-11，-1，1，11，再由a＜b＜c＜d得出每个数，求出答案．
解答：解：已知a、b、c、d是互不相等的整数，且abcd=121，
又121=11×11，那么a，b，c，d四个整数之积等于121，
只有，-11，-1，1，11，
又已知a＜b＜c＜d，
所以，a=-11，b=-1，c=1，d=11，
那么，ac+bd=（-11）1+（-1）11=-11-1=-12．
故答案为：-12．
又121=11×11，那么a，b，c，d四个整数之积等于121，
只有，-11，-1，1，11，
又已知a＜b＜c＜d，
所以，a=-11，b=-1，c=1，d=11，
那么，ac+bd=（-11）1+（-1）11=-11-1=-12．
故答案为：-12．
点评：此题考查的知识点是整数问题的综合运用，解答此题的关键是由121=11×11和abcd=121，得出四个数的值．
练习册系列答案
英才点津系列答案
红果子三级测试卷系列答案
课堂练加测系列答案
相关题目
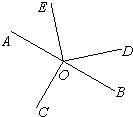20、如图，点O是直线AB上一点，OC平分∠AOB，在直线AB另一侧以O为顶点作∠DOE=90°
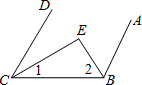已知，如图CE，BE分别平分∠DCB，∠ABC，若要使AB∥CD，则∠1与∠2应满足的关系是