Question

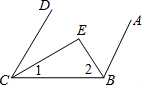
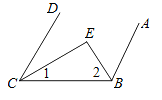
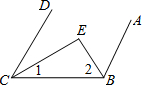已知，如图CE，BE分别平分∠DCB，∠ABC，若要使AB∥CD，则∠1与∠2应满足的关系是

互余

．

Answer 1

分析：根据角平分线的性质有∠1=

1

2

∠DCB，∠2=

1

2

∠ABC，再根据平行线的判定得到当∠DCB+∠ABC=180°时，AB∥CD，则∠1+∠2=

1

2

×180°=90°．

解答：解：∵CE，BE分别平分∠DCB，∠ABC，
∴∠1=

1

2

∠DCB，∠2=

1

2

∠ABC，
当∠DCB+∠ABC=180°时，AB∥CD，
∴∠1+∠2=

1

2

×180°=90°，
即∠1与∠2互余时，AB∥CD．
故答案为互余．

点评：本题考查了平行线的判定：同旁内角互补，两直线平行．也考查了角平分线的性质．