Question

【题目】我们规定：对于已知线段，若存在动点（点不与、重合），始终满足，则称是“雅动三角形”，其中，点为“雅动点”，为它的“雅动值”．

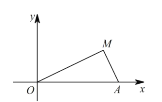
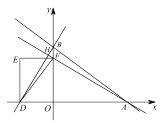
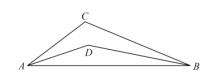
图1 图2 图3

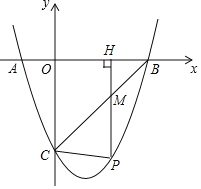
（1）如图1，为坐标原点，点坐标是，的“雅动值”为，当时，请直接写出这个三角形的周长；

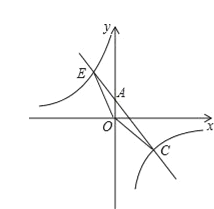
（2）如图2，已知四边形是矩形，点、的坐标分别是、，直线（且）交、轴于、两点，连接、并延长交于点，问：是否为“雅动三角形”？如果是，请求出它的“雅动值”；如果不是，请说明理由；

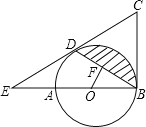
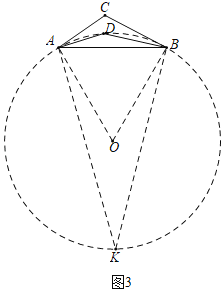
（3）如图3，已知（是常数且），点是平面内一动点且满足，若、的平分线交于点，问：点的运动轨迹长度是否为定值？如果是，请求出它的轨迹长度；如果不是，请说明理由．

Answer 1

【答案】（1）；（2）是“雅动三角形”，”雅动值”是；（3）点的运动轨迹长度为定值，定值为.

【解析】

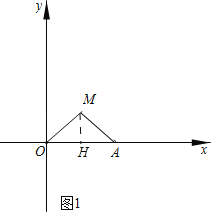
(1)如图1中，作于．根据等腰直角三角形的性质解决问题即可．

（2）由一次函数解析式求出AB点坐标（用含b的式子表示）再利用线段比证明三角形相似，然后利用相似三角形的性质证明即可．

（3）构造过A、B、D三点的圆，证明D在圆周上，求出圆心角，半径，利用弧长公式计算，即可解决问题．

解：（1）如图1中，作于．

，

，

，，

，

，

，

的周长为．

故答案为：.

（2）结论：是“雅动三角形”，”雅动值”是．

如图2中，

点、的坐标分别是、，

，，

对于直线，令，得到，令，得到，

，

，

，

，

，，

，

，

，

直线且交、轴于、两点，连接、并延长交于点，

是“雅动三角形”，”雅动值”是．

（3）点的运动轨迹长度为定值，运动路径的长．

理由如下：

如图3中，以为边向下作等边，以为圆心，为半径作，在上三点下方取一点，连接，．

，平分，平分，

，

，

，

，，，四点共圆，

点的运动轨迹是，

点的运动轨迹长度为定值，运动路径的长．