题目内容
已知多项式ax3+bx2-47x-15可被3x+1和2x-3整除,则a+b= .
【答案】分析:因为多项式ax3+bx2-47x-15可被3x+1和2x-3整除,则说明(3x+1)、(2x-3)都是多项式ax3+bx2-47x-15的一个因式,故使(3x+1)、(2x-3)等于0的数必是多项式ax3+bx2-47x-15的解,即把(3x+1)=0、(2x-3)=0求出的x的值代入多项式,即得到关于a、b的二元一次方程,解即可,从而可求出a+b.
解答:解:由已知可知, 得
得
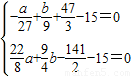 ,
,
解得 ,
,
∴a+b=24+2=26.
点评:本题考查的是多项式除以多项式,注意理解整除的含义,比如A被B整除,另外一层意思也就是说,B是A的公因式,使公因式B等于0的值,必是A的一个解.
解答:解:由已知可知,
 得
得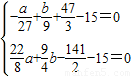 ,
,解得
 ,
,∴a+b=24+2=26.
点评:本题考查的是多项式除以多项式,注意理解整除的含义,比如A被B整除,另外一层意思也就是说,B是A的公因式,使公因式B等于0的值,必是A的一个解.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目