��Ŀ����
��2012•������ͼ����ƽ��ֱ������ϵ�з���һֱ�����ǰ壬�䶥��ΪA��0��1����B��2��0����O��0��0����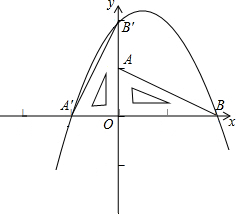 �������ǰ���ԭ��O��ʱ����ת90�㣬�õ���A��B��O��
�������ǰ���ԭ��O��ʱ����ת90�㣬�õ���A��B��O��
��1��һ�����߾�����A�䡢B�䡢B����������ߵĽ���ʽ��
��2�����P���ڵ�һ�������������ϵ�һ���㣬�Ƿ���ڵ�P��ʹ�ı���PB��A��B������ǡ�A��B��O���4���������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3���ڣ�2���������£���ָ���ı���PB��A��B��������״���ı��Σ���д���ı���PB��A��B���������ʣ�
 �������ǰ���ԭ��O��ʱ����ת90�㣬�õ���A��B��O��
�������ǰ���ԭ��O��ʱ����ת90�㣬�õ���A��B��O����1��һ�����߾�����A�䡢B�䡢B����������ߵĽ���ʽ��
��2�����P���ڵ�һ�������������ϵ�һ���㣬�Ƿ���ڵ�P��ʹ�ı���PB��A��B������ǡ�A��B��O���4���������ڣ������P�����ꣻ�������ڣ���˵�����ɣ�
��3���ڣ�2���������£���ָ���ı���PB��A��B��������״���ı��Σ���д���ı���PB��A��B���������ʣ�
��������1��������ת�����ʵó�A�䣨-1��0����B�䣨0��2���������ô���ϵ��������κ�������ʽ���ɣ�
��2������S�ı���PB��A��B=S��B��OA��+S��PB��O+S��POB���ټ����ı���PB��A��B������ǡ�A��B��O�����4�����ó�һԪ���η��̣��ó�P�����꼴�ɣ�
��3������P�������Լ�B�����꼴�ɵó��ı���PB��A��BΪ�������Σ����õ����������ʵó��𰸼��ɣ�
��2������S�ı���PB��A��B=S��B��OA��+S��PB��O+S��POB���ټ����ı���PB��A��B������ǡ�A��B��O�����4�����ó�һԪ���η��̣��ó�P�����꼴�ɣ�
��3������P�������Լ�B�����꼴�ɵó��ı���PB��A��BΪ�������Σ����õ����������ʵó��𰸼��ɣ�
����⣺��1����A��B��O���ɡ�ABO��ԭ��O��ʱ����ת90��õ��ģ�
��A��0��1����B��2��0����O��0��0����
��A�䣨-1��0����B�䣨0��2����----------��1�֣�
����һ��
�������ߵĽ���ʽΪ��y=ax2+bx+c��a��0����
�������߾�����A�䡢B�䡢B��
��
��
��ã�
��
�����������������ߵĽ���ʽΪy=-x2+x+2��----------��3�֣�
����������A�䣨-1��0����B�䣨0��2����B��2��0����
�������ߵĽ���ʽΪ��y=a��x+1����x-2��
��B�䣨0��2������ó���2=a��0+1����0-2����
��ã�a=-1��
�����������������ߵĽ���ʽΪy=-��x+1����x-2��=-x2+x+2��
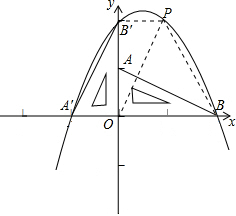
��2����PΪ��һ�������������ϵ�һ���㣬
��P��x��y������x��0��y��0��P����������y=-x2+x+2��
����PB��PO��PB�䣬
��S�ı���PB��A��B=S��B��OA��+S��PB��O+S��POB��
=
��1��2+
��2��x+
��2��y��
=x+��-x2+x+2��+1��
=-x2+2x+3��----------��5�֣�
��A��O=1��B��O=2�����A��B��O�����
��1��2=1��
�����ı���PB��A��B������ǡ�A��B��O�����4������
4=-x2+2x+3��
��x2-2x+1=0��
��ã�x1=x2=1��
��ʱy=-12+1+2=2����P��1��2����----------��7�֣�
����ڵ�P��1��2����ʹ�ı���PB��A��B������ǡ�A��B��O�����4����----------��8�֣�
��3���ı���PB��A��BΪ�������Σ��𰸲�Ψһ�����������е�����2�����ɣ�
�ٵ�������ͬһ���ϵ������ڽ���ȣ��ڵ������ζԽ�����ȣ�
�۵��������ϵ����µ�ƽ�У��ܵ�������������ȣ�----------��10�֣�
���÷��ű�ʾ��
�١�B��A��B=��PBA����A��B��P=��BPB�䣻��PA��=B��B����B��P��A��B����B��A��=PB��----------��10�֣�
��A��0��1����B��2��0����O��0��0����
��A�䣨-1��0����B�䣨0��2����----------��1�֣�
����һ��
�������ߵĽ���ʽΪ��y=ax2+bx+c��a��0����
�������߾�����A�䡢B�䡢B��
��
|
��ã�
|
�����������������ߵĽ���ʽΪy=-x2+x+2��----------��3�֣�
����������A�䣨-1��0����B�䣨0��2����B��2��0����
�������ߵĽ���ʽΪ��y=a��x+1����x-2��
��B�䣨0��2������ó���2=a��0+1����0-2����
��ã�a=-1��
�����������������ߵĽ���ʽΪy=-��x+1����x-2��=-x2+x+2��

��2����PΪ��һ�������������ϵ�һ���㣬
��P��x��y������x��0��y��0��P����������y=-x2+x+2��
����PB��PO��PB�䣬
��S�ı���PB��A��B=S��B��OA��+S��PB��O+S��POB��
=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=x+��-x2+x+2��+1��
=-x2+2x+3��----------��5�֣�
��A��O=1��B��O=2�����A��B��O�����
| 1 |
| 2 |
�����ı���PB��A��B������ǡ�A��B��O�����4������
4=-x2+2x+3��
��x2-2x+1=0��
��ã�x1=x2=1��
��ʱy=-12+1+2=2����P��1��2����----------��7�֣�
����ڵ�P��1��2����ʹ�ı���PB��A��B������ǡ�A��B��O�����4����----------��8�֣�
��3���ı���PB��A��BΪ�������Σ��𰸲�Ψһ�����������е�����2�����ɣ�
�ٵ�������ͬһ���ϵ������ڽ���ȣ��ڵ������ζԽ�����ȣ�
�۵��������ϵ����µ�ƽ�У��ܵ�������������ȣ�----------��10�֣�
���÷��ű�ʾ��
�١�B��A��B=��PBA����A��B��P=��BPB�䣻��PA��=B��B����B��P��A��B����B��A��=PB��----------��10�֣�
������������Ҫ�����˶��κ������ۺ�Ӧ���Լ������������ʵ�֪ʶ�������ı���PB��A��B������ǡ�A��B��O�����4���ó���ʽ�������x�ǽ���ؼ���

��ϰ��ϵ�д�
 ����ͬ�����Ծ�ϵ�д�
����ͬ�����Ծ�ϵ�д�
�����Ŀ
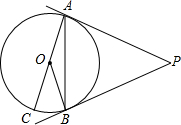 ��2012•������ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬AC�ǡ�O��ֱ��������P=46�㣬���BAC=
��2012•������ͼ��PA��PB�ǡ�O�����ߣ�A��BΪ�е㣬AC�ǡ�O��ֱ��������P=46�㣬���BAC=
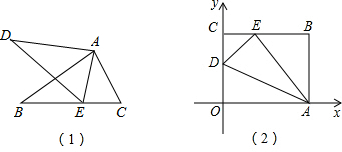
 ��2012•������ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC�͡�DEF�Ķ��㶼�ڸ���ϣ�P1��P2��P3��P4��P5�ǡ�DEF���ϵ�5����㣬�밴Ҫ��������и��⣺
��2012•������ͼ���ڱ߳�Ϊ1��С��������ɵ������У���ABC�͡�DEF�Ķ��㶼�ڸ���ϣ�P1��P2��P3��P4��P5�ǡ�DEF���ϵ�5����㣬�밴Ҫ��������и��⣺