题目内容
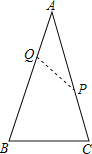
【题目】有一张等腰三角形纸片,AB=AC=5,BC=3,小明将它沿虚线PQ剪开,得到△AQP和四边形BCPQ两张纸片(如图所示),且满足∠BQP=∠B,则下列五个数据![]() ,3,
,3,![]() ,2,
,2,![]() 中可以作为线段AQ长的有_____个.
中可以作为线段AQ长的有_____个.
【答案】3.
【解析】
解:作CD∥PQ,交AB于D,如图所示:
则∠CDB=∠BQP,∵AB=AC=5,∴∠B=∠ACB,∵∠BQP=∠B,∴∠B=∠ACB=∠CDB,∴CD=BC=3,△BCD∽△BAC,∴![]() ,即
,即![]() ,解得:BD=
,解得:BD=![]() ,∴AD=AB﹣BD=
,∴AD=AB﹣BD=![]() ,∵CD∥PQ,∴△APQ∽△ACD,∴
,∵CD∥PQ,∴△APQ∽△ACD,∴![]() ,即
,即![]() ,解得:AP=
,解得:AP=![]() AQ,当AQ=
AQ,当AQ=![]() 时,AP=
时,AP=![]() ×
×![]() =
=![]() >5,不合题意,舍去;
>5,不合题意,舍去;
当AQ=3时,AP=![]() ×3=
×3=![]() <5,符合题意;
<5,符合题意;
当AQ=![]() 时,点P与C重合,不合题意,舍去;
时,点P与C重合,不合题意,舍去;
当AQ=2时,AP=![]() ×2=
×2=![]() <5,符合题意;
<5,符合题意;
当AQ=![]() 时,AP=
时,AP=![]() ×
×![]() =
=![]() <5,符合题意;
<5,符合题意;
综上所述:可以作为线段AQ长的有3个;
故答案为:3.


练习册系列答案
相关题目