题目内容
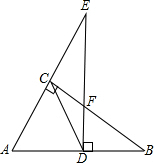 已知,如图,在Rt△ABC中,CD是斜边上的中线,DE⊥AB交BC于点F,交AC的延长线于点E.
已知,如图,在Rt△ABC中,CD是斜边上的中线,DE⊥AB交BC于点F,交AC的延长线于点E.(1)△ADE∽△FDB吗?为什么?
(2)你能推出结论CD2=DE•DF吗?请试一试.
分析:(1)根据题意,得∠A+∠B=90°,∠A+∠E=90°,则∠E=∠B,易证△ADE∽△FDB;
(2)由Rt△ABC中,CD是斜边上的中线,得CD=DB,则∠DCB=∠DBC,又∠E=∠B,所以∠BCD=∠E,又∠CDF是公共角,所以△CFD∽△ECD,即可得出;
(2)由Rt△ABC中,CD是斜边上的中线,得CD=DB,则∠DCB=∠DBC,又∠E=∠B,所以∠BCD=∠E,又∠CDF是公共角,所以△CFD∽△ECD,即可得出;
解答:证明:(1)∵DE⊥AB,BC⊥AE,
∴∠A+∠B=90°,∠A+∠E=90°,
∴∠E=∠B,
∴△ADE∽△FDB(AA);
(2)∵CD为Rt△ABC的中线,
∴CD=DB=AD,
∴∠DCB=∠DBC,
又∠E=∠B,
∴∠BCD=∠E,
又∠CDF是公共角,
∴△CFD∽△ECD,
∴
=
,即CD2=DE•DF.
∴∠A+∠B=90°,∠A+∠E=90°,
∴∠E=∠B,
∴△ADE∽△FDB(AA);
(2)∵CD为Rt△ABC的中线,
∴CD=DB=AD,
∴∠DCB=∠DBC,
又∠E=∠B,
∴∠BCD=∠E,
又∠CDF是公共角,
∴△CFD∽△ECD,
∴
| CD |
| DE |
| DF |
| CD |
点评:本题主要考查了直角三角形和相似三角形的判定与性质,掌握直角三角形斜边上的中线等于斜边的一半,是解答本题的关键.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
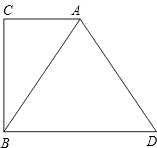 已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由.
已知:如图,在Rt△ABC中,∠C=90°,过点B作BD∥AC,且BD=2AC,连接AD.试判断△ABD的形状,并说明理由. (1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD.
(1997•陕西)已知,如图,在Rt△ABC中,∠C=90°,以AC为直径的⊙O交斜边AB于E,OD∥AB.求证:①ED是⊙O的切线;②2DE2=BE•OD. (2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE.
(2013•丰台区一模)已知:如图,在Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连结DE. 已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y.
已知:如图,在Rt△ABC中,∠C=90°,BC=4,AC=8,点D在斜边AB上,分别作DE⊥AC,DF⊥BC,垂足分别为E、F,得四边形DECF,设DE=x,DF=y. 已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.
已知,如图,在Rt△ABC中,∠C=90°,AC=15,BC=20,求斜边AB上的高CD.