题目内容
【题目】如图,抛物线y=ax2+ ![]() x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).
x+c(a≠0)与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴交x轴于点D,已知点A的坐标为(﹣1,0),点C的坐标为(0,2).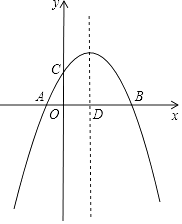
(1)求抛物线的解析式;
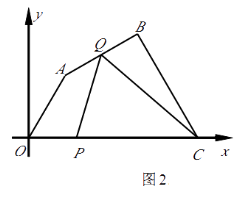
(2)在抛物线的对称轴上是否存在点P,使△PCD是以CD为腰的等腰三角形?如果存在,直接写出P点的坐标;如果不存在,请说明理由;
(3)点E是线段BC上的一个动点,过点E作x轴的垂线与抛物线相交于点F,当点E运动到什么位置时,四边形CDBF的面积最大?求出四边形CDBF的最大面积及此时E点的坐标.
【答案】
(1)
解:由题意  ,
,
解得 ![]() ,
,
∴二次函数的解析式为y=﹣ ![]() x2+
x2+ ![]() x+2
x+2
(2)
解:存在.如图1中,
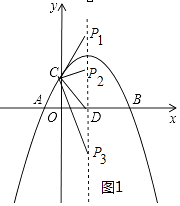
∵C(0,2),D( ![]() ,0),
,0),
∴CD= ![]() =
= ![]() ,
,
当CP=CD时,P1( ![]() ,4),
,4),
当DP=DC时,P2( ![]() ,
, ![]() ),P3(
),P3( ![]() ,﹣
,﹣ ![]() ).
).
综上所述,满足条件的点P坐标为( ![]() ,4)或(
,4)或( ![]() ,
, ![]() )或(
)或( ![]() ,﹣
,﹣ ![]()
(3)
解:如图2中,作CM⊥EF于M,

∵B(4,0),C(0,2),
∴直线BC的解析式为y=﹣ ![]() ,设E(a,﹣
,设E(a,﹣ ![]() +2),F(a,﹣
+2),F(a,﹣ ![]() a2+
a2+ ![]() a+2),
a+2),
∴EF=﹣ ![]() a2+
a2+ ![]() a+2﹣(﹣
a+2﹣(﹣ ![]() +2)=﹣
+2)=﹣ ![]() a2+2a,(0≤a≤4),
a2+2a,(0≤a≤4),
∵S四边形CDBF=S△BCD+S△CEF+S△BEF= ![]() BDOC+
BDOC+ ![]() EFCM+
EFCM+ ![]() EFBN
EFBN
= ![]() +
+ ![]() a(﹣
a(﹣ ![]() a2+2a)+
a2+2a)+ ![]() (4﹣a)(﹣
(4﹣a)(﹣ ![]() a2+2a)
a2+2a)
=﹣a2+4a+ ![]()
=﹣(a﹣2)2+ ![]() ,
,
∴a=2时,四边形CDBF的面积最大,最大值为 ![]() ,
,
∴E(2,1)
【解析】(1)利用待定系数法转化为解方程组即可.(2)如图1中,分两种情形讨论①当CP=CD时,②当DP=DC时,分别求出点P坐标即可.(3)如图2中,作CM⊥EF于M,设E(a,﹣ ![]() +2),F(a,﹣
+2),F(a,﹣ ![]() a2+
a2+ ![]() a+2),则EF=﹣
a+2),则EF=﹣ ![]() a2+
a2+ ![]() a+2﹣(﹣
a+2﹣(﹣ ![]() +2)=﹣
+2)=﹣ ![]() a2+2a,(0≤a≤4),根据S四边形CDBF=S△BCD+S△CEF+S△BEF=
a2+2a,(0≤a≤4),根据S四边形CDBF=S△BCD+S△CEF+S△BEF= ![]() BDOC+
BDOC+ ![]() EFCM+
EFCM+ ![]() EFBN,构建二次函数,利用二次函数的性质即可解决问题.
EFBN,构建二次函数,利用二次函数的性质即可解决问题.
【考点精析】掌握二次函数的图象和二次函数的性质是解答本题的根本,需要知道二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点;增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某市甲、乙两个汽车销售公司,去年一至十月份每月销售同种品牌汽车的情况如图所示:
![]() 请你根据上图填写下表:
请你根据上图填写下表:
销售公司 | 平均数 | 方差 | 中位数 | 众数 |
甲 |
| 9 | ||
乙 | 9 |
| 8 |
![]() 请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
请你从以下两个不同的方面对甲、乙两个汽车销售公司去年一至十月份的销售情况进行分析:
![]() 从平均数和方差结合看;
从平均数和方差结合看;
![]() 从折线图上甲、乙两个汽车销售公司销售数量的趋势看
从折线图上甲、乙两个汽车销售公司销售数量的趋势看![]() 分析哪个汽车销售公司较有潜力
分析哪个汽车销售公司较有潜力![]() .
.