Question

【题目】如图，在平面直角坐标系中，点P从原点O出发，每次向上平移2个单位长度或向右平移1个单位长度．

（1）实验操作：

在平面直角坐标系中描出点P从点O出发，平移1次后，2次后，3次后可能到达的点，并把相应点的坐标填写在表格中：

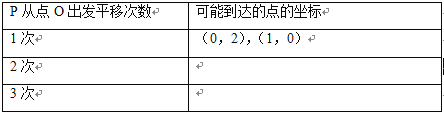
（2）观察发现：

设点P（x，y），任一次平移，点P可能到达的点的纵、横坐标都满足一定的关系式.

例如：平移1次后2x+y= _________；平移2次后2x+y= ；平移3次后2x+y= ；……由此我们知道，平移n次后点P的坐标都满足一定的关系式是 ；

（3）探索运用：

点P从点O出发经过n次平移后到达点Q，若点Q的纵坐标比横坐标大6，并且P平移的路径长不小于50，不超过56，请直接写出Q的坐标．

Answer 1

【答案】（1）（0，4），（1，2），（2，0）；（0，6），（1，4），（2，2），（3，0）.

（2）2，4，6 2x +y=2n．

（3）点Q的坐标为（22，28），（24，30）．

【解析】试题分析：1、根据点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度,结合点的平移的相关知识,即可确定平移后的点可能的坐标；

2、观察图形可知任意一次平移,点P可能到达的点构成的函数图象形如一次函数;

3、令平移1次后的函数解析式为y1=k1×x+b1(k1≠0),平移2次后的函数解析式为y2=k2×x+b2(k2≠0),再将对应点的坐标代入函数解析式求解即可得出第(2)问前两空的答案,综合前两空的答案可得最后一空的答案；

4、对于第(3)问,结合上述结论,可得点P平移n次后的点构成的函数,结合纵坐标比横坐标大6，即可确定点Q的坐标。

试题解析：

(1)点P从原点O出发,每次向上平移2个单位长度或向右平移1个单位长度,

平移1次后,可能达到点A、B,其中A(0,2)、B(1,0);

平移2次后,可能达到点C、D、E,其中C(0,4)、D(1,2)、E(2,0);

平移3次后,可能达到点F、G、H、I,其中F(0,6)、G(1,4)、H(2,2)、I(3,0).

填表略.

(2)观察发现,任意一次平移,点P可能到达的点构成的函数图象形如一次函数,

令平移1次后的函数解析式为y1=k1×x+b1(k1≠0),平移2次后的函数解析式为y2=k2×x+b2(k2≠0)

∵ A(0,2)、B(1,0)在y1=k1×x+b1图象上

∴2=b10=k1+b1

解得:b1=2k1=2

∴y1=2x+2

故平移1次后的点在函数y=-2x+2的图象上.；

∵ C(0,4)、D(1,2)、E(2,0)在y2=k2×x+b2图象上

∴ 将点C、点E的坐标代入y2=k2×x+b2,得

4=b2，2=k2+b2

解得:b2=4k2=2

∴y2=2x+4

将D(1,2)代入上式,满足,故平移2次后的点在函数y=-2x+4的图象上.

综上,可知平移n次后对应的点在函数y=-2x+2n的图象上.

(3) 设点Q的横坐标为x，则纵坐标为x+6.

由题意知∴.

∵点Q的坐标为正整数，∴当x=22,23,24,25时，对应y=28,29,30,31.

由2x +y=2n，得为整数.∴y=28或30.

∴点Q的坐标为（22，28），（24，30）．