题目内容
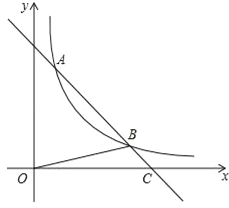
【题目】如图所示,梯形![]() 中,
中,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,点
,点![]() 是边
是边![]() 上的动点,点
上的动点,点![]() 是射线
是射线![]() 上一点,射线
上一点,射线![]() 和射线
和射线![]() 交于点
交于点![]() ,且
,且![]() .
.

(1)求线段![]() 的长;
的长;
(2)如果![]() 是以
是以![]() 为腰的等腰三角形,求线段
为腰的等腰三角形,求线段![]() 的长;
的长;
(3)如果点![]() 在边
在边![]() 上(不与点
上(不与点![]() 、
、![]() 重合),设
重合),设![]() ,
,![]() ,求
,求![]() 关于
关于![]() 的函数解析式,并写出
的函数解析式,并写出![]() 的取值范围;
的取值范围;
【答案】(1)7;(2)15或![]() ;(3)
;(3)![]() (
(![]() ).
).
【解析】
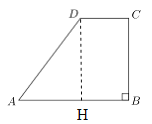
试题分析:(1)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() ,由勾股定理求出AH的长,进而求出DC的长;
,由勾股定理求出AH的长,进而求出DC的长;
(2)可证![]() ∽
∽![]() ,从而得到
,从而得到![]() 是以
是以![]() 为腰的等腰三角形,分两种情况讨论:① 若
为腰的等腰三角形,分两种情况讨论:① 若![]() ,② 若
,② 若![]() ;
;
(3)表示出DE的长,由![]() ∽
∽![]() ,得出EG的长,从而得出DG的长,由DF∥AE,得到
,得出EG的长,从而得出DG的长,由DF∥AE,得到![]() ,化简即可得到结论.
,化简即可得到结论.
试题解析:(1)过点![]() 作
作![]() ,垂足为点
,垂足为点![]() .在Rt
.在Rt![]() 中,
中,![]() ,
,![]() ,
,![]() ,∴
,∴![]() .又∵
.又∵![]() ,∴
,∴![]() ;
;
(2)∵![]() ,又
,又![]() ,∴
,∴![]() ∽
∽![]() .由
.由![]() 是以
是以![]() 为腰的等腰三角形,可得
为腰的等腰三角形,可得![]() 是以
是以![]() 为腰的等腰三角形.
为腰的等腰三角形.
① 若![]() ,∵
,∵![]() ,∴
,∴![]() ;
;
② 若![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,∴
,∴![]() .
.
在Rt![]() 中,
中,![]() ,
,![]() ;
;
在Rt![]() 中,
中,![]() ,
,![]() ,∴
,∴![]() ;
;
综上所述:当![]() 是以
是以![]() 为腰的等腰三角形时,线段
为腰的等腰三角形时,线段![]() 的长为15或
的长为15或![]() ;
;
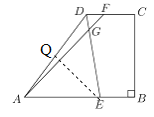
(3)在Rt![]() 中,
中,![]() ,
,![]() .∵
.∵![]() ∽
∽![]() ,∴
,∴![]() ,∴
,∴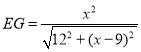 ,∴
,∴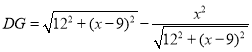 .∵
.∵![]() ∥
∥![]() ,∴
,∴![]() ,
,![]() ,∴
,∴![]() ,
,![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目