Question

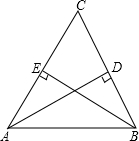
AB是⊙O的直径，点E是半圆上一动点（点E与点A、B都不重合），点C是BE延长线上的一点，且CD⊥AB，垂足为D，CD与AE交于点H，点H与点A不重合．
（1）求证：△AHD∽△CBD；
（2）连HO，若CD=AB=2，求HD+HO的值．

Answer 1

（1）证明：AB是⊙O的直径
∴∠AEB=90°，则∠ABC+∠BAE=90°，
又∵CD⊥AB，
∴∠BAE+∠AHD=90°，
∴∠AHD=∠ABC，
又∵∠ADH=∠CDB=90°，
∴△AHD∽△CBD．

（2）设OD=x，则BD=1-x，AD=1+x，
∵Rt△AHD∽Rt△CBD，
则HD：BD=AD：CD，
即HD：（1-x）=（1+x）：2，
即HD=

1-x2

2

，
在Rt△HOD中，由勾股定理得：
OH=

OD2+HD2

=

x2+( 1-x2 2 )2

=

1+x2

2

，
所以HD+HO=

1-x2

2

+

1+x2

2

=1；
②当点E移动到使D与O重合的位置时，这时HD与HO重合，由Rt△AHO∽Rt△CBO，利用对应边的比例式为方程，可以算出HD=HO=

1

2

，即HD+HO=1；
③当D在OA段时BD=1+x，AD=1-x，证明同①∵Rt△AHD∽Rt△CBD，
则HD：BD=AD：CD，
即HD：（1-x）=（1+x）：2，
即HD=

1-x2

2

，
在Rt△HOD中，由勾股定理得：
OH=

OD2+HD2

=

x2+( 1-x2 2 )2

=

1+x2

2

，
所以HD+HO=

1-x2

2

+

1+x2

2

=1．