Question

【题目】如图，△ABC和△CDE都是等边三角形，B，C，D三点在一条直线上，AD与BE交于点P，AC，BE交于点M，AD，CE交于点N，连接MN，则下列五个结论：①AD=BE；②∠BMC=∠ANE；③∠APM=60°；④AN=BM；⑤△CMN是等边三角形．其中一定正确的是__________．（填出所有正确结论的序号）

Answer 1

【答案】①③④⑤

【解析】

根据先证明△BCE≌△ACD，得出AD=BE，根据已知给出的条件即可得出答案．

∵△ABC和△DEC都是等边三角形，∴AC=BC，CD=CE，∠ACB=∠ECD=60°，∴∠ACB+∠ACE=∠ECD+∠ACE，即∠BCE=∠ACD，∴△BCE≌△ACD（SAS），∴AD=BE，故①正确；

∵△BCE≌△ACD，∴∠CBE=∠CAD．

∵∠ACB=∠ACE=60°，∴∠BMC=∠ANC，故②错误；

∵△BCE≌△ACD，∴∠CBE=∠CAD．

∵∠BMC=∠AMP，∴∠APM=∠ACB=60°，故③正确；

在△ACN和△BCM中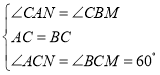，∵，∴△ACN≌△BCM，∴AN=BM，故④正确；

△ACN≌△BCM，∴CM=CN，∴△CMN为等腰三角形．

∵∠MCN=60°，∴△CMN是等边三角形，故⑤正确．

故答案为：①③④⑤．