Question

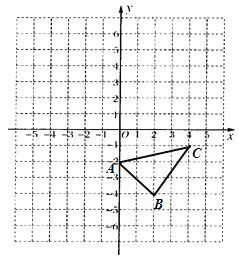
【题目】如图，在平面坐标系中，ΔABC是等腰直角三角形，∠ABC=90°，AB=BC，点A坐标为（-8，-3），点B坐标为（0，-5），AC交x轴于点D.

（1）求点C和D的坐标；

（2）点M在x轴上，当ΔAMB的周长最小时，求点M的坐标.

Answer 1

【答案】（1）C（2，3），D（-3，0）；（2）M（-5，0）.

【解析】

（1）分别作AF⊥y轴，CE⊥y轴，垂足为F,E，证明△AFB≌△CEB，得BE=AF=8，CE=BF=2，又OB=5，从而可得点C 的坐标，设AC的直线解析式为y=kx+b，把A，C点的坐标分别代入直线解析式，求出k和b的值，令y=0，求出x的值即可；

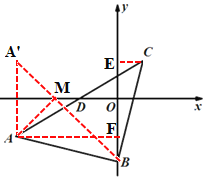
（2）作A点关于x轴的对称点A‘，连接A’B交x轴于点M，此时ΔAMB的周长最小，设直线A’B的解析式为y=ax+b，把A’，B点的坐标分别代入，求出其解析式，令y=0，求出x的值即可.

（1）分别作AF⊥y轴，CE⊥y轴，垂足为F，E，

∴∠AFB=∠BEC=90°，

∴∠BAF+∠ABF=90°, ∠CBE+∠BCE=90°，

∵∠ABF+∠CBE=∠ABC=90°

∴∠ABF=∠BCE，

∵AB=BC，

∴△ABF≌△BCE，

∴BE=AF，CE=BF

∵A（-8，-3），B（0，-5），

∴AF=8，OF=3，OB=5，

∴OE=3,CE=2，

∴C点坐标为（2，3）;

设直线AC的关系式为y=kx+b，把A（-8，-3），C（2，3）分别代入得，

，

解得，，

所以，直线AC的解析式为：，

令y=0，则有，解得，x=-3，

∴D点坐标为（-3，0）；

（2）如图，作A点关于x轴的对称点A‘，连接A’B交x轴于点M，此时ΔAMB的周长最小，

设直线A’B的解析式为y=ax+b，把A’（-8，3），B(0,-5)分别代入解析式得，

，

解得，

所以，直线A’B的解析式为：y=-x-5，

令y=0，则x=-5，

所以，M点的坐标为（-5，0）.